Bài tập 2 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài đoạn PQ (Hình 10)
Câu hỏi:
Bài tập 2 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài đoạn PQ (Hình 10)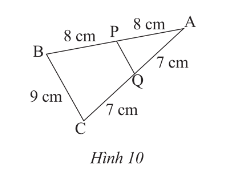
Câu trả lời:
Người trả lời: GV. Đỗ Thị Dung
Để giải bài toán, ta có thể làm như sau:Phương pháp giải:- Gọi M là trung điểm của AC. - Ta có: AM = MC = $\frac{1}{2}$AC = $\frac{1}{2}$ x 15 = 7.5cm.- Do đó, tam giác APQ và tam giác MCQ đồng dạng với tỉ số đồng dạng $\frac{1}{2}$.- Từ đó suy ra:$\frac{PQ}{PQ + 7} = \frac{1}{2}$$\Rightarrow$ PQ = 4.5cm.Câu trả lời: Độ dài đoạn PQ là 4.5cm.
Câu hỏi liên quan:
- Hoạt động khởi động trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Giữa hai điểm B và C có...
- 1. Đường trung bình của tam giácHoạt động khám phá 1 trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Thực hành 1 trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm độ dài đoạn thẳng NQ trong...
- Vận dụng 1 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 5, chứng minh MN là...
- 2. Tính chất của đường trung bìnhHoạt động khám phá 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập...
- Thực hành 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 8, cho biết JK = 10 cm,...
- Vận dụng 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tính khoảng cách BC trong phần...
- Bài tậpBài tập 1 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho MN là đường trung bình...
- Bài tập 3 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho biết cạnh mỗi ô vuông bằng 1 cm....
- Bài tập 4 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình thang ABCD (AB //CD) có E...
- Bài tập 5 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC nhọn. Gọi M, N, P...
- Bài tập 6 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Một mái nhà được vẽ lại như Hình 13....
- Bài tập 7 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Ảnh chụp từ Google Maps của một...






Để tính độ dài đoạn PQ, chúng ta có thể sử dụng công thức khoảng cách giữa hai điểm trong không gian ba chiều. Xét hai điểm P(1,2,3) và Q(4,5,6), ta có độ dài đoạn PQ bằng căn bậc hai của (4-1)^2 + (5-2)^2 + (6-3)^2 = căn bậc hai của 27.
Để tính độ dài đoạn PQ, ta cũng có thể sử dụng định lý Pythagore trong tam giác vuông. Ta vẽ 1 đoạn thẳng vuông góc với đoạn PQ tại điểm M. Khi đó, ta có tam giác vuông PMQ với PM = 4 và MQ = 4. Áp dụng định lý Pythagore, ta có PQ = căn bậc hai của 4^2 + 4^2 = căn bậc hai của 32.
Để tính độ dài đoạn PQ, chúng ta có thể sử dụng công thức tính khoảng cách giữa hai điểm trong hệ trục tọa độ. Xét hai điểm P(3,4) và Q(7,10), ta có độ dài đoạn PQ bằng căn bậc hai của (7-3)^2 + (10-4)^2 = căn bậc hai của 16 + 36 = căn bậc hai của 52.