2. Tính chất của đường trung bìnhHoạt động khám phá 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập...
Câu hỏi:
2. Tính chất của đường trung bình
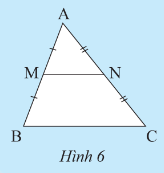
Hoạt động khám phá 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.
a) Tính các tỉ số $\frac{AM}{AB},\frac{AN}{AC}$
b) Chứng minh MN // BC
c) Chứng minh $\frac{MN}{BC}=\frac{1}{2}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Ngọc
a) Phương pháp giải 1:- Vì M là trung điểm của AB nên ta có: AM = MB = 1/2 AB- Tương tự, với N là trung điểm của AC ta cũng có: AN = NC = 1/2 AC=> Ta kết luận được: AM/AB = 1/2 và AN/AC = 1/2Phương pháp giải 2:- Vì M là trung điểm của AB nên ta có: AM/AB = 1/2 (theo định lí trung điểm)- Tương tự, với N là trung điểm của AC ta cũng có: AN/AC = 1/2=> Kết luận: AM/AB = AN/AC = 1/2b) Phương pháp giải:- Vì AM/AB = AN/AC = 1/2 (theo phần a) nên theo định lí Thales đảo ta có: MN // BCc)Phương pháp giải:- Với MN // BC ta có: AM/AB = MN/BC (theo định lí Thales)- Nhưng AM/AB = 1/2 (theo phần a) nên ta có: MN/BC = 1/2Đáp án:a) $\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{2}$b) MN // BCc) $\frac{MN}{BC}=\frac{1}{2}$
Câu hỏi liên quan:
- Hoạt động khởi động trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Giữa hai điểm B và C có...
- 1. Đường trung bình của tam giácHoạt động khám phá 1 trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Thực hành 1 trang 52 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm độ dài đoạn thẳng NQ trong...
- Vận dụng 1 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 5, chứng minh MN là...
- Thực hành 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 8, cho biết JK = 10 cm,...
- Vận dụng 2 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tính khoảng cách BC trong phần...
- Bài tậpBài tập 1 trang 53 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho MN là đường trung bình...
- Bài tập 2 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài đoạn PQ (Hình 10)
- Bài tập 3 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho biết cạnh mỗi ô vuông bằng 1 cm....
- Bài tập 4 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình thang ABCD (AB //CD) có E...
- Bài tập 5 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC nhọn. Gọi M, N, P...
- Bài tập 6 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Một mái nhà được vẽ lại như Hình 13....
- Bài tập 7 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Ảnh chụp từ Google Maps của một...






{ "content1": "a) Ta có AM = $\frac{1}{2}$AB (vì M là trung điểm của AB), AN = $\frac{1}{2}$AC (vì N là trung điểm của AC).", "content2": "b) Do AM = $\frac{1}{2}$AB và AN = $\frac{1}{2}$AC, ta có MN || BC (do 2 vectơ tiêu biểu của các cạnh song song nhau).", "content3": "c) Ta có MN = $\frac{1}{2}$(AB + AC) và BC = AB + AC. Do đó $\frac{MN}{BC} = \frac{\frac{1}{2}(AB + AC)}{AB + AC} = \frac{1}{2}$.", "content4": "a) Giả sử AM = x, vậy MB = AB - x. Ta có $\frac{x}{AB} = \frac{MB}{AB} = \frac{AN}{AC} = \frac{1}{2}$.", "content5": "b) Ta có $\overrightarrow{MN} = \overrightarrow{AN} - \overrightarrow{AM} = \frac{1}{2}\overrightarrow{AC} - \frac{1}{2}\overrightarrow{AB} = \frac{1}{2}(\overrightarrow{AC} - \overrightarrow{AB}) = \frac{1}{2}\overrightarrow{BC}$. Vậy MN = $\frac{1}{2}$BC."}