Bài 3: Quan sát Hình 9a) Hai góc aOg và cOe có phải là hai góc đối đỉnh không? Vì sao?b) Tìm các...
Câu hỏi:
Bài 3: Quan sát Hình 9
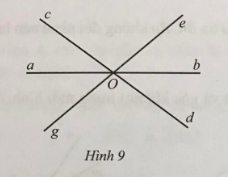
a) Hai góc aOg và cOe có phải là hai góc đối đỉnh không? Vì sao?
b) Tìm các cặp góc đối đỉnh (khác góc bẹt và góc không) ở Hình 9.
c) Chứng tỏ rằng $\widehat{aOg}+\widehat{cOe}+\widehat{bOd}=180^{\circ}$
Câu trả lời:
Người trả lời: GV. Đỗ Thị Ngọc
a) Để xác định hai góc aOg và cOe có phải là hai góc đối đỉnh không, chúng ta cần quan sát xem hai tia aO và Oc có cắt nhau không. Nếu hai tia aO và Oc không cắt nhau tại một điểm chung, tức là không tạo thành một góc, thì hai góc aOg và cOe không phải là hai góc đối đỉnh.b) Các cặp góc đối đỉnh trong Hình 9 là: - aOc và bOd - cOe và dOg - bOe và aOg - aOe và bOg - bOc và aOd - cOg và dOec) Ta có $\widehat{aOc}=\widehat{bOd}$ (hai góc đối đỉnh) nên ta có: $\widehat{aOg}+\widehat{cOe}+\widehat{bOd}$ $=\widehat{aOg}+\widehat{aOc}+\widehat{cOe}$ $=\widehat{eOg}$ $= 180^{\circ}$Vậy câu trả lời đầy đủ và chi tiết là:a) Hai góc aOg và cOe không là hai góc đối đỉnh vì Og và Oe là hai tia đối nhưng Oa và Oc không là hai tia đối.b) Các cặp góc đối đỉnh là aOc và bOd, cOe và dOg, bOe và aOg, aOe và bOg, bOc và aOd, cOg và dOe.c) Ta có $\widehat{aOc}=\widehat{bOd}$ (hai góc đối đỉnh) nên $\widehat{aOg}+\widehat{cOe}+\widehat{bOd}=\widehat{aOg}+\widehat{aOc}+\widehat{cOe}=\widehat{eOg}= 180^{\circ}$
Câu hỏi liên quan:
- BÀI TẬPBài 1: Quan sát Hình 8 và chỉ ra:a) Bốn cặp góc kề nhaub) Ba cặp góc kề bùc) Hai cặp góc đối...
- Bài 2: Cho các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau. Tìm số đo góc aOc, bOc, bOd, aOd...
- Bài 4: Quan sát hình 10 và chỉ ra:a) Bốn góc kề với góc AOC (không kể góc bẹt)b) Hai góc kề bù với...
- Bài 5: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?a) Hai góc đối đỉnh thì bằng...
- Bài 6: Quan sát hình 11. Tính số đo mỗi góc xOy, yOz biết...
- Bài 7: Quan sát hình 12. Cho hai góc xOy, yOz là hai góc kề nhau, $\widehat{xOz}=150^{\circ} $và...






{ "content1": "a) Hai góc aOg và cOe không phải là hai góc đối đỉnh. Vì góc aOg và cOe không cùng nằm trên cùng một đường thẳng.", "content2": "b) Các cặp góc đối đỉnh khác góc bẹt và góc không ở Hình 9 là: aOd và eOc, bOd và cOe, aOc và gOd, aOe và gOc.", "content3": "c) Chứng minh $\widehat{aOg}+\widehat{cOe}+\widehat{bOd}=180^{\circ}$: Ta có góc aOg và bOd là góc đối đỉnh với nhau, bOd và cOe là cặp góc đối đỉnh, cOe và aOg cũng là cặp góc đối đỉnh. Do đó, tổng của ba góc này sẽ bằng 180 độ theo tính chất của góc phụ." }