4.58.Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP...
Câu hỏi:
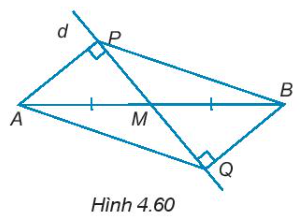
4.58. Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP, BQ (P $\in $ d, Q $\in $ d) vuông góc với đường thẳng d (H.4.60). Chứng minh rằng:
a) AP = BQ.
b) $\Delta APB=\Delta BQA$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Long
Phương pháp giải:a) Ta xét tam giác vuông PAM và tam giác vuông QBM. Với M là trung điểm của AB, ta có AM = BM. Đồng thời, vì đường thẳng d không vuông góc với AB nên hai góc PMA và QMB đều nhọn và bằng nhau.Từ đó, theo trường hợp cạnh-huyền-góc, ta có $\Delta PAM = \Delta QBM$.Do đó, AP = BQ.b) Tiếp tục xét tam giác APB và tam giác BQA. Ta đã chứng minh được AP = BQ. Hai tam giác có cạnh chung AB và hai góc đối nhau PAB và QBA cũng bằng nhau do $\Delta PAM = \Delta QBM$.Do đó, theo trường hợp cạnh-góc-cạnh, ta có $\Delta APB = \Delta BQA$.Vậy, ta đã chứng minh được cả hai phần câu hỏi.Câu trả lời:a) AP = BQb) $\Delta APB = \Delta BQA$
Câu hỏi liên quan:
- A. CÂU HỎI (TRẮC NGHIỆM)1.Trong các câu sau đây, câu nào đúng?A. Mọi tam giác có ít nhất một...
- 2.Trong các câu sau đây, câu nàosai?A. Tổng số đo ba góc trong một tam giác bằng $18...
- 3.Trong các câu sau đây, câu nào đúng?A. Hai tam giác có ba cặp góc tương ứng bằng nhau là...
- 4.Trong các câu sau đây, câu nàosai?A. Hai tam giác có hai cặp cạnh tương ứng bằng nhau...
- 5.Trong các câu sau đây, câu nào đúng?A. Tam giác có ba cạnh bằng nhau là tam giác đều.B. Tam...
- 6.Trong các câu sau đây, câu nàosai?A. Tam giác tù là tam giác có một góc có số đo lớn...
- 7.Trong các câu sau đay, câu nào đúng?A. Đường thẳng đi qua trung điểm của đoạn AB là đường...
- B. BÀI TẬP4.51.Tính số đo các góc x, y, z, t, v trong Hình 4.55
- 4.52.Trong các câu sau đây, câu nào đúng, câu nào sai?a) Tam giác nhọn có ba góc đều nhọn.b)...
- 4.53.Trong các câu sau đây, câu nào đúng, câu nào sai?a) Tam giác cân có một góc bằng 6...
- 4.54.Tính số đo các góc chưa biết của các tam giác dưới đây (H.4.56).
- 4.55.Cho các điểm A, B, C, D như Hình 4.57.a) Chứng minh rằng $\widehat{DAC}=\widehat{DBC}$b)...
- 4.56.Cho các điểm A, B, C, D, E, F như Hình 4.58.a)Tìm ba cặp tam giác vuông bằng nhau...
- 4.57.Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các...
- 4.59.Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.
- 4.60.Cho hình thang cân ABCD có đáy lớn AD, đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2...






{ "content1": "Ta có AM = MB vì d đi qua trung điểm M của AB. Gọi O là giao điểm của d và AB, ta có AO = BO vì d không vuông góc với AB. Do đó, tam giác AOM và BOM đều là tam giác vuông cân. Khi đó, AP = AO = BO = BQ.", "content2": "Gọi x là độ dài của AM = MB = PQ. Ta có APB và AQB đều là tam giác vuông cân tại P và Q, nên $\Delta APB$ = 2*$\Delta APQ$ = 2*(1/2*AP*PQ) = AP*PQ = x*x = x^2. Tương tự, $\Delta BQA$ = BQ*PQ = x*x = x^2. Vậy $\Delta APB$ = $\Delta BQA$.", "content3": "Gọi h là độ dài từ P đến d, khi đó h là độ cao của tam giác APB và cũng là độ cao của tam giác BQA. Ta có $\Delta APB$ = 1/2*AP*h = 1/2*PQ*h = 1/2*x*x = x^2/2. Tương tự, $\Delta BQA$ = 1/2*BQ*h = 1/2*PQ*h = 1/2*x*x = x^2/2. Vậy $\Delta APB$ = $\Delta BQA$.", "content4": "Kẻ dọc từ M vuông góc với AB, gọi I là giao điểm của dọc đó với d. Ta có MI = MB do M là trung điểm của AB, cũng có MI = AP do dọc từ M vuông góc với AB và AP vuông góc với d. Vậy ta có AP = MB = BQ. Ta cũng thấy là cả $\Delta APB$ và $\Delta BQA$ đều có cạnh cặp AB, cạnh cặp đứng và cạnh chéo bằng nhau, nên theo đẳng thức các tam giác cân, $\Delta APB$ = $\Delta BQA$."}