4.56.Cho các điểm A, B, C, D, E, F như Hình 4.58.a)Tìm ba cặp tam giác vuông bằng nhau...
Câu hỏi:
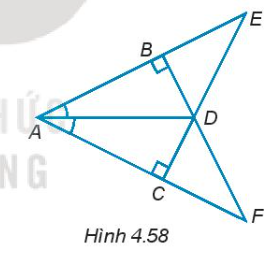
4.56. Cho các điểm A, B, C, D, E, F như Hình 4.58.
a) Tìm ba cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
b) Chứng minh $\Delta ADE=\Delta ADF$.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Ánh
a) Phương pháp giải:
Để tìm ba cặp tam giác vuông bằng nhau, ta cần xác định các tam giác có cùng một cặp góc vuông và cạnh huyền bằng nhau. Sau đó, chứng minh bằng cách so sánh các cạnh và góc khác.
- Xét tam giác vuông ABD và tam giác vuông ACD
+ AD: cạnh chung
+ $\widehat{BAD}=\widehat{CAD}$ (giả thiết)
⇒ $\Delta ABD = \Delta ACD$ (cạnh huyền - góc nhọn)
- Xét tam giác vuông ABF và tam giác vuông ACE
+ AB = AC (do $\Delta ABD = \Delta ACD$)
+ $\widehat{FAB}=\widehat{EAC}$ (góc chung)
⇒ $\Delta ABF = \Delta ACE$ (cạnh góc vuông và góc nhọn kề)
- Xét tam giác vuông BDE và tam giác vuông CDF
+ BD = CD (do $\Delta ABD = \Delta ACD$)
+ $\widehat{BDE}=\widehat{CDF}$ (hai góc đối đỉnh)
⇒ $\Delta BDE = \Delta CDF$ (cạnh góc vuông và góc nhọn kề)
Vậy ta có ba cặp tam giác vuông bằng nhau như trên.
b) Phương pháp chứng minh $\Delta ADE = \Delta ADF$:
- Xét tam giác ADE và tam giác ADF
+ AE = AF (do $\Delta ABF = \Delta ACE$)
+ $\widehat{EAD}=\widehat{FAD}$ (giả thiết)
+ AD: cạnh chung
⇒ $\Delta ADE = \Delta ADF$ (cạnh giữa - góc - cạnh)
Vậy, chúng ta đã chứng minh được rằng hai tam giác ADE và ADF bằng nhau.
Để tìm ba cặp tam giác vuông bằng nhau, ta cần xác định các tam giác có cùng một cặp góc vuông và cạnh huyền bằng nhau. Sau đó, chứng minh bằng cách so sánh các cạnh và góc khác.
- Xét tam giác vuông ABD và tam giác vuông ACD
+ AD: cạnh chung
+ $\widehat{BAD}=\widehat{CAD}$ (giả thiết)
⇒ $\Delta ABD = \Delta ACD$ (cạnh huyền - góc nhọn)
- Xét tam giác vuông ABF và tam giác vuông ACE
+ AB = AC (do $\Delta ABD = \Delta ACD$)
+ $\widehat{FAB}=\widehat{EAC}$ (góc chung)
⇒ $\Delta ABF = \Delta ACE$ (cạnh góc vuông và góc nhọn kề)
- Xét tam giác vuông BDE và tam giác vuông CDF
+ BD = CD (do $\Delta ABD = \Delta ACD$)
+ $\widehat{BDE}=\widehat{CDF}$ (hai góc đối đỉnh)
⇒ $\Delta BDE = \Delta CDF$ (cạnh góc vuông và góc nhọn kề)
Vậy ta có ba cặp tam giác vuông bằng nhau như trên.
b) Phương pháp chứng minh $\Delta ADE = \Delta ADF$:
- Xét tam giác ADE và tam giác ADF
+ AE = AF (do $\Delta ABF = \Delta ACE$)
+ $\widehat{EAD}=\widehat{FAD}$ (giả thiết)
+ AD: cạnh chung
⇒ $\Delta ADE = \Delta ADF$ (cạnh giữa - góc - cạnh)
Vậy, chúng ta đã chứng minh được rằng hai tam giác ADE và ADF bằng nhau.
Câu hỏi liên quan:
- A. CÂU HỎI (TRẮC NGHIỆM)1.Trong các câu sau đây, câu nào đúng?A. Mọi tam giác có ít nhất một...
- 2.Trong các câu sau đây, câu nàosai?A. Tổng số đo ba góc trong một tam giác bằng $18...
- 3.Trong các câu sau đây, câu nào đúng?A. Hai tam giác có ba cặp góc tương ứng bằng nhau là...
- 4.Trong các câu sau đây, câu nàosai?A. Hai tam giác có hai cặp cạnh tương ứng bằng nhau...
- 5.Trong các câu sau đây, câu nào đúng?A. Tam giác có ba cạnh bằng nhau là tam giác đều.B. Tam...
- 6.Trong các câu sau đây, câu nàosai?A. Tam giác tù là tam giác có một góc có số đo lớn...
- 7.Trong các câu sau đay, câu nào đúng?A. Đường thẳng đi qua trung điểm của đoạn AB là đường...
- B. BÀI TẬP4.51.Tính số đo các góc x, y, z, t, v trong Hình 4.55
- 4.52.Trong các câu sau đây, câu nào đúng, câu nào sai?a) Tam giác nhọn có ba góc đều nhọn.b)...
- 4.53.Trong các câu sau đây, câu nào đúng, câu nào sai?a) Tam giác cân có một góc bằng 6...
- 4.54.Tính số đo các góc chưa biết của các tam giác dưới đây (H.4.56).
- 4.55.Cho các điểm A, B, C, D như Hình 4.57.a) Chứng minh rằng $\widehat{DAC}=\widehat{DBC}$b)...
- 4.57.Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các...
- 4.58.Cho đường thẳng d đi qua trung điểm M của đoạn thẳng AB và không vuông góc với AB. Kẻ AP...
- 4.59.Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.
- 4.60.Cho hình thang cân ABCD có đáy lớn AD, đáy nhỏ BC thỏa mãn AD = 4 cm và AB = BC = CD = 2...






a) Tam giác ADE và tam giác ADF bằng nhau vì chúng có cạnh chung AD, góc vuông tại A và cạnh đối diện với góc vuông là DE và DF. Đồng thời, cả hai tam giác đều có diện tích bằng nhau do cơ sở và chiều cao bằng nhau.
b) Ta có thể chứng minh tam giác ADE bằng tam giác ADF bằng cách sử dụng định lí cạnh-góc-cạnh (C-G-C). Với DE=DF (hai cạnh) và góc E = góc F (góc vuông), ta suy ra hai tam giác đó bằng nhau.
a) Tam giác ADE và tam giác ADF bằng nhau vì chúng có cạnh chung AD, góc vuông tại A và cạnh đối diện với góc vuông là DE và DF. Do đó, chúng đều có hai cạnh và góc giống nhau nên bằng nhau.
b) Để chứng minh tam giác ADE bằng tam giác ADF, ta cần chứng minh DE=DF và góc E bằng góc F. Ta có DE=DF vì chúng là cạnh của tam giác vuông ADE và tam giác vuông ADF. Góc E bằng góc F vì chúng là góc vuông của hai tam giác đó.
a) Có ba cặp tam giác vuông bằng nhau là tam giác ADE và tam giác ADF vì chúng có cạnh chung AD, góc vuông tại A và cạnh đối diện với góc vuông là DE và DF. Hai tam giác ADE và ADF có cùng cạnh AD, cùng góc A và cùng góc D nên chúng bằng nhau.