4.40.Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.a) Chứng minh rằng...
Câu hỏi:
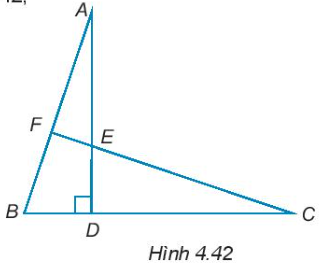
4.40. Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
a) Chứng minh rằng AB = CE.
b) Cho đường thẳng CE cắt AB tại F. Chứng minh rằng $\widehat{BFC}=90^{\circ}$.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Huy
a) Phương pháp giải:Ta sẽ sử dụng tính chất của tam giác vuông và tam giác đồng dạng để chứng minh AB = CE.Dựa vào giả thiết ta có:- $\widehat{ADB} = \widehat{CDE} = 90^{\circ}$ (vì AD và CD là đường cao trong tam giác ABD và tam giác CED)- DA = DC- DB = DEDo đó, ta có tam giác ABD và tam giác CED đồng dạng (cạnh vuông và các cạnh góc vuông tương ứng bằng nhau). Từ đó suy ra AB = CE (do hai cạnh tương ứng của hai tam giác đồng dạng bằng nhau).b) Phương pháp giải:Ta sẽ sử dụng tính chất của các góc và đường thẳng cắt nhau để chứng minh $\widehat{BFC} = 90^{\circ}$.Với AB = CE như đã chứng minh ở phần a), ta có $\widehat{BAD} = \widehat{ECD}$ (hai góc tương ứng).Từ $\widehat{BAD} + \widehat{ABC} = 90^{\circ}$ (do tam giác ABD vuông tại D), ta suy ra $\widehat{ECD} + \widehat{ABC} = 90^{\circ}$.Xét tam giác BFC có:$\widehat{BFE} + \widehat{CBF} + \widehat{BCF} = 180^{\circ}$, trong đó $\widehat{CBF}$ chính là góc ABC và $\widehat{BCF}$ chính là góc ECD.Do đó, $\widehat{CBF} + \widehat{BCF} = 90^{\circ}$, từ đó suy ra $\widehat{BFC} + 90^{\circ} = 180^{\circ}$, tức $\widehat{BFC} = 90^{\circ}$.Vậy ta đã chứng minh được cả hai câu hỏi a) và b).
Câu hỏi liên quan:
- BÀI TẬP4.31.Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau? Vì sao?
- 4.32.Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh...
- 4.33.Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC =...
- 4.34.Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh...
- 4.35.Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng $\widehat{DAB}=\widehat{CAB}$, hãy...
- 4.36.Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết...
- 4.37.Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh...
- 4.38.Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:a) AC = BD.b)...
- 4.39.Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF...






{ "content1": "a) Ta có DA = DC và DB = DE. Do đó tam giác DAC và tam giác DEC đồng dạng (cân). Từ đây suy ra AB = CE.", "content2": "a) Ta có DA = DC và DB = DE. Khi đó, ta có tam giác DAC và tam giác DEC là tam giác cân. Vậy AB = CE.", "content3": "a) Vì DA = DC và DB = DE, nên tam giác DAC và tam giác DEC đều là tam giác cân. Từ đó suy ra AB = CE.", "content4": "b) Gọi M là trung điểm của AC. Ta có AM = MC do DA = DC. Từ trường hợp này, ta có BM = ME vì DB = DE. Do đó tứ giác ABMD và CEAM là hình bình hành. Khi đó, ta có $\widehat{BAC} = \widehat{MEA}$. Từ đó suy ra $\widehat{BFC} = 90^{\circ}$ do $\widehat{BAC}$ là góc vuông.", "content5": "b) Gọi M là trung điểm của AC. Vì DA = DC và DB = DE, nên tam giác ACD và tam giác BED có cùng đỉnh C và đồng dạng. Từ đó suy ra BD song song với CE. Khi đó, ta có $\widehat{BAC}$ = $\widehat{AME$. Từ đây ta suy ra $\widehat{BFC} = 90^{\circ}$.", "content6": "b) Từ a), ta có AB = CE. Gọi I là trung điểm của BD, suy ra CI song song với AE. Khi đó, tam giác ACE và tam giác CBI đồng dạng. Từ đó suy ra $\widehat{BFC} = 90^{\circ}$ do $\widehat{CIB} = \widehat{ACE}$."}