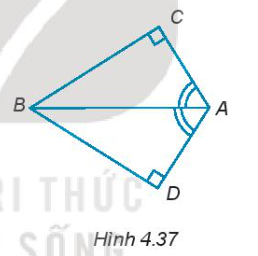
4.35.Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng $\widehat{DAB}=\widehat{CAB}$, hãy...
Câu hỏi:
4.35. Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng $\widehat{DAB}=\widehat{CAB}$, hãy chứng minh CB = DB.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hưng
Để chứng minh CB = DB, ta xét tam giác ABC và tam giác ABD. Trong tam giác ABC và ABD:- AB là cạnh chung.- $\widehat{CAB} = \widehat{DAB}$ (giả thiết)- $\widehat{ACB} = \widehat{ADB} = 90^\circ$ (giả thiết)Do đó, ta có $\Delta ABC = \Delta ABD$ (cạnh huyền - góc nhọn).Vậy, CB = DB.
Câu hỏi liên quan:
- BÀI TẬP4.31.Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau? Vì sao?
- 4.32.Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh...
- 4.33.Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC =...
- 4.34.Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh...
- 4.36.Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết...
- 4.37.Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh...
- 4.38.Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:a) AC = BD.b)...
- 4.39.Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF...
- 4.40.Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.a) Chứng minh rằng...






Khi đó, theo định lý nối tiếp, ta có CB = DB.
Do đó, ta có AC/AD = EC/ED. Kết hợp với AC/AD = CB/DB, ta suy ra CB/DB = EC/ED.
Gọi điểm E trên AB sao cho BE song song với AC, ta có tứ giác ADEC là tứ giác điều hòa.
Từ đó, ta suy ra DB = CB*(AD/AC)
Do đó, ta có tỉ số cạnh AD/AC = DB/CB (vì cạnh tương ứng đồng dạng nhau)