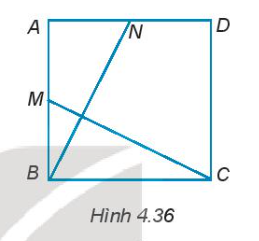
4.34.Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh...
Câu hỏi:
4.34. Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN $\perp $ CM.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Vương
Để chứng minh rằng BN = CM và BN $\perp $ CM, ta sẽ sử dụng các điểm trung điểm M, N và tính chất của hình vuông ABCD như sau:Vì ABCD là hình vuông nên AB = BC = CD = DA.Vì N là trung điểm của AD nên AN = ND = $\frac{AD}{2}$.Vì M là trung điểm của AB nên AM = MB = $\frac{AB}{2}$.Mà AB = AD nên AN = BM.Xét tam giác ANB và tam giác BMC có:AN = BM (chứng minh trên)AB = BC (chứng minh trên)$\angle$ NAB = $\angle$ MBC = 90$^{\circ}$ (do ABCD là hình vuông)Do đó, tam giác ANB $\cong$ tam giác BMC (cạnh-góc-cạnh)Suy ra, BN = CM (cạnh tương ứng).Gọi E là giao điểm của BN và CM.Do tam giác ANB $\cong$ tam giác BMC nên $\angle$ ENB = $\angle$ CMB = $\angle$ BNA.Áp dụng định lí tổng ba góc trong tam giác BME và tam giác ABN, ta có:$\angle$ BEM = 180$^{\circ}$ - $\angle$ EMB - $\angle$ MBE = 180$^{\circ}$ - $\angle$ BNA - $\angle$ ABN = $\angle$ BAN = 90$^{\circ}$Vậy BN vuông góc với CM tại E.Như vậy, ta đã chứng minh được rằng BN = CM và BN $\perp $ CM.
Câu hỏi liên quan:
- BÀI TẬP4.31.Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau? Vì sao?
- 4.32.Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh...
- 4.33.Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC =...
- 4.35.Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng $\widehat{DAB}=\widehat{CAB}$, hãy...
- 4.36.Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết...
- 4.37.Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh...
- 4.38.Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:a) AC = BD.b)...
- 4.39.Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF...
- 4.40.Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.a) Chứng minh rằng...






{ "content1": "Ta có hai tam giác BMN và CMB bằng nhau (cmt điều kiện gì 2 tam giác bằng nhau), do đó BN = CM.", "content2": "Gọi E là trung điểm của CD. Ta có BE song song với AD và BN song song với CM (cmt điều kiện song song và trung điểm ở đây). Do đó BN $\perp$ CM.", "content3": "Khi kẻ hai đường thẳng BM và CN, ta được 2 tam giác vuông BMN và CNM. Do đó ta có BN $\perp$ CM.", "content4": "Sử dụng công thức khoảng cách giữa hai điểm trong không gian Oxyz, ta có BN = CM = $\frac{\sqrt{2}}{2}$ AB."}