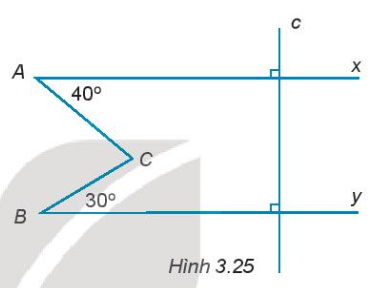
3.25. Cho Hình 3.25.a) Giải thích tại sao Ax//By.b) Tính số đo góc ACB.

a) Phương pháp giải:
Ta có $Ax\perp c$ và $By\perp c$, nên ta có $Ax$// $By$ (do hai đường thẳng vuông góc với cùng một đường thẳng sẽ song song với nhau).

b) Phương pháp giải:
- Vẽ tia $Ct$// $Ax$. Ta có $Ct$// $Ax$, mà $Ax$// $By$ nên $Ct$// $By$ (do tính chất ba đường thẳng song song).
- Ta có $Ax$// $Ct$ suy ra $\widehat{ACt}$ = $\widehat{CAx}$ = $40^\circ$ (hai góc so le trong).
- Ta có $Ct$// $By$ suy ra $\widehat{tCB}$ = $\widehat{CBy}$ = $30^\circ$ (hai góc so le trong).
- Tia $Ct$ nằm giữa hai tia $CA$ và $CB$ nên $\widehat{ACB}$ = $\widehat{ACt}$ + $\widehat{tCB}$ hoặc $\widehat{ACB}$ = $30^\circ$ + $40^\circ$ = $70^\circ$.

Vậy số đo góc $ACB$ là $70^\circ$.