3.21.Cho đường thẳng xx', điểm A thuộc xx'. Trên tia Ax' lấy điểm B (điểm B khác điểm A). Vẽ...
Câu hỏi:
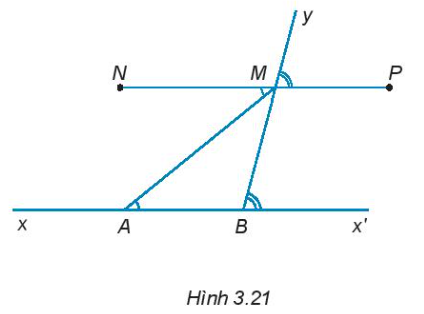
3.21. Cho đường thẳng xx', điểm A thuộc xx'. Trên tia Ax' lấy điểm B (điểm B khác điểm A). Vẽ tia By, trên tia By lấy điểm m. Hai điểm N và P thỏa mãn $\widehat{NMA}=\widehat{MAB},\widehat{PMy}=\widehat{MBx'}$ (H.3.21). Giải thích tại sao ba điểm N, M, P thẳng hàng.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Huy
Phương pháp giải:Để chứng minh ba điểm N, M, P thẳng hàng, ta sử dụng các tiên đề sau:1. Hai góc cùng ngoại tiếp bằng nhau.2. Hai góc tương đương bằng nhau.3. Điểm nằm trên đường thẳng song song với một đường thẳng đã cho là thẳng hàng với điểm đó.Giả sử MN và MP không thẳng hàng, ta cần chứng minh rằng giả thiết này dẫn đến mâu thuẫn.- Ta có $\widehat{NMA}=\widehat{MAB}$ từ tiên đề (1) về hai góc cùng ngoại tiếp chúng nhau.- Ta có $\widehat{PMy}=\widehat{MBx'}$ từ tiên đề (2) về hai góc tương đương.- Vì MN // xx' và MP // xx', nên theo tiên đề (3), ta có hai đường thẳng MN và MP trùng nhau.- Điều này dẫn đến mâu thuẫn với giả thiết ban đầu.Do đó, ba điểm N, M, P phải thẳng hàng.Vậy, N, M, P thẳng hàng.
Câu hỏi liên quan:
- BÀI TẬP3.18.Cho Hình 3.19, biết a // b.a) Tính số đo góc A1.b) So sánh góc A4 và góc B2.c)...
- 3.19.Vẽ lại Hình 3.20 vào vở.a) Giải thích tại sao Ax // By.b) Tính số đo góc ABy'.c) Tính số...
- 3.20.Trong các phát biểu sau, phát biểu nào diễn đạt đúng nội dung của tiên đề Euclid?a) Qua...
- 3.22.Vẽ lại Hình 3.22 vào vở.a) Giải thích tại sao a//b.b) Tính số đo góc ABH.
- 3.23. Vẽ lại Hình 3.23 vào vở. Giải thích tại sao:a) xx'//yy'b) $xx'\perp a$
- 3.24.Cho Hình 3.24.a) Giải thích tại sao yy'//zz'.b) Tính số đo góc ABz.c) Vẽ tia phân giác...
- 3.25. Cho Hình 3.25.a) Giải thích tại sao Ax//By.b) Tính số đo góc ACB.
- 3.26. Cho Hình 3.26, Biết Ax//Dy, $\widehat{xAC}=50^{\circ},\widehat{ACD}=110^{\circ}$. Tính số đo...
Bình luận (0)





