3.19.Vẽ lại Hình 3.20 vào vở.a) Giải thích tại sao Ax // By.b) Tính số đo góc ABy'.c) Tính số...
Câu hỏi:
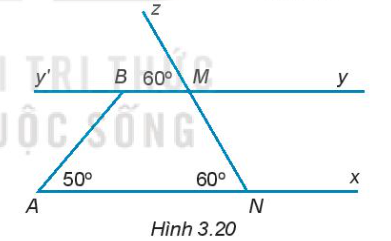
3.19. Vẽ lại Hình 3.20 vào vở.
a) Giải thích tại sao Ax // By.
b) Tính số đo góc ABy'.
c) Tính số đo góc ABM.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Hạnh
a) Phương pháp giải:Ta có $\widehat{BMz}=\widehat{ANM}(=60^{\circ})$. Hai góc này ở vị trí đồng vị nên Ax // By (dấu hiệu nhận biết hai đường thẳng song song).b) Phương pháp giải:Ta có Ax//By. Suy ra $\widehat{ABy'}=\widehat{BAN}$ (hai góc so le trong), do đó $\widehat{ABy'}=50^{\circ}.c) Phương pháp giải:Ta có $\widehat{ABM}+\widehat{ABy'}=180^{\circ}$ (hai góc kề bù) hay $\widehat{ABM}+50^{\circ}=180^{\circ}$. Do đó $\widehat{ABm}=130^{\circ}.Đáp án:a) Ta có Ax // By.b) Góc ABy' có số đo là 50 độ.c) Góc ABM có số đo là 130 độ.
Câu hỏi liên quan:
- BÀI TẬP3.18.Cho Hình 3.19, biết a // b.a) Tính số đo góc A1.b) So sánh góc A4 và góc B2.c)...
- 3.20.Trong các phát biểu sau, phát biểu nào diễn đạt đúng nội dung của tiên đề Euclid?a) Qua...
- 3.21.Cho đường thẳng xx', điểm A thuộc xx'. Trên tia Ax' lấy điểm B (điểm B khác điểm A). Vẽ...
- 3.22.Vẽ lại Hình 3.22 vào vở.a) Giải thích tại sao a//b.b) Tính số đo góc ABH.
- 3.23. Vẽ lại Hình 3.23 vào vở. Giải thích tại sao:a) xx'//yy'b) $xx'\perp a$
- 3.24.Cho Hình 3.24.a) Giải thích tại sao yy'//zz'.b) Tính số đo góc ABz.c) Vẽ tia phân giác...
- 3.25. Cho Hình 3.25.a) Giải thích tại sao Ax//By.b) Tính số đo góc ACB.
- 3.26. Cho Hình 3.26, Biết Ax//Dy, $\widehat{xAC}=50^{\circ},\widehat{ACD}=110^{\circ}$. Tính số đo...






c) Góc ABM và góc B của tam giác ABM và tam giác BMy là góc ngoại tiếp cùng nhau nên số đo của góc ABM là số đo của góc B, tức là 45 độ.
b) Góc ABy' và góc ABy là góc so le với cùng một cạnh AB nên số đo của góc ABy' cũng là 70 độ.
a) Vì tam giác ABx và tam giác BMy có cặp đường bằng nhau là By và AB nên theo thuộc tính của tam giác đồng dạng, ta có Ax // By.
c) Góc ABM và góc YBM là góc đồng quy với hai cạnh cắt nhau (AB và BM) nên số đo của góc ABM là số đo của góc YBM, tức là 45 độ.
b) Góc ABy' và góc B là góc đồng quy với hai cạnh cắt nhau (AB và By') nên số đo của góc ABy' là số đo của góc B, tức là 70 độ.