I. Mô tả ba đường conic dựa trên tiêu điểm và đường chuẩnHoạt động:Quan sát Hình 22a, Hình...
Câu hỏi:
I. Mô tả ba đường conic dựa trên tiêu điểm và đường chuẩn
Hoạt động: Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
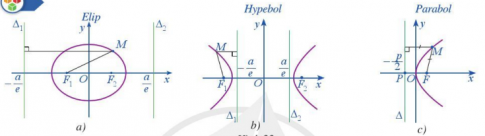
Câu trả lời:
Người trả lời: GV. Đỗ Thị Long
Để giải câu hỏi trên, ta có thể thực hiện như sau:Phương pháp giải:1. Xác định phương trình của đường conic (elip, hyperbol hay parabol) dựa trên tiêu điểm và đường chuẩn.2. Từ phương trình của đường conic, đặt điểm M(x, y) vào phương trình và tìm các điểm F1, F2 là tiêu điểm và Δ là đường chuẩn mà M thuộc về.3. Tính khoảng cách từ điểm M đến tiêu điểm F và khoảng cách từ điểm M đến đường chuẩn Δ.4. Tính tỉ số giữa khoảng cách từ M đến F và M đến Δ, ta sẽ được giá trị của e.Câu trả lời:- Đối với mỗi điểm M thuộc elip (E) có phương trình $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ (với a > b > 0) thì ta có $\frac{MF}{d(M,\Delta)} = e$ (trong đó 0 < e < 1), với F là một trong hai tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm F.- Đối với mỗi điểm M thuộc hyperbol (H) có phương trình $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ (với a > 0, b > 0) thì ta có $\frac{MF}{d(M,\Delta)} = e$ (trong đó e > 1), với F là một trong hai tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm F.- Đối với mỗi điểm M thuộc parabol (P) có phương trình y^2 = 2px (với p > 0) thì ta có $\frac{MF}{d(M,\Delta)} = 1$, với F là tiêu điểm và Δ là đường chuẩn ứng với tiêu điểm F.
Câu hỏi liên quan:
- Bài tậpBài tập 1.Cho hình chữ nhật ABCD với bốn đỉnh A(–4; 3), B(4; 3), C(4; –3), D(–4;...
- Bài tập 2.Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các...
- Bài tập 3.Cho parabol có phương trình chính tắc y$^{2}$= 2x. Tìm tiêu điểm, phương...
- Bài tập 4.Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm...
- Bài tập 5.Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của...
- Bài tập 6.Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có...
- Bài tập 7.Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).Với...
Bình luận (0)





