Bài tập 7.Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).Với...
Câu hỏi:
Bài tập 7. Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39).
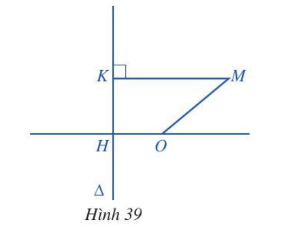
Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho $MK^{2} – MO^{2} = 1$ là một đường parabol.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Đạt
Để giải bài toán này, ta có thể sử dụng phương pháp định lí hình chiếu vuông góc. Ta chọn hệ trục toạ độ sao cho điểm O trùng với gốc toạ độ và trục Ox trùng với đường thẳng OH. Giả sử M có tọa độ (x; y) thì K có tọa độ là (-1; y) vì K là hình chiếu vuông góc của M lên Δ theo định lí trên.Khi đó, ta có:$MK^{2} - MO^{2} = 1$$\Leftrightarrow {(x-(-1))^{2} + (y-y)^{2}} - [(0-x)^{2} + (0-y)^{2}] = 1$$\Leftrightarrow {(x+1)^{2} + 0^{2}} - [x^{2} + y^{2}] = 1$$\Leftrightarrow (x^{2} + 2x + 1) - (x^{2} + y^{2}) = 1$$\Leftrightarrow 2x + 1 - y^{2} = 1$$\Leftrightarrow y^{2} = 2x$Vậy tập hợp các điểm M là một đường parabol có phương trình $y^{2} = 2x$. Như vậy, câu trả lời cho câu hỏi trên là: "Tập hợp các điểm M trong mặt phẳng sao cho $MK^{2} - MO^{2} = 1$ là một đường parabol có phương trình $y^{2} = 2x.$"
Câu hỏi liên quan:
- I. Mô tả ba đường conic dựa trên tiêu điểm và đường chuẩnHoạt động:Quan sát Hình 22a, Hình...
- Bài tậpBài tập 1.Cho hình chữ nhật ABCD với bốn đỉnh A(–4; 3), B(4; 3), C(4; –3), D(–4;...
- Bài tập 2.Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các...
- Bài tập 3.Cho parabol có phương trình chính tắc y$^{2}$= 2x. Tìm tiêu điểm, phương...
- Bài tập 4.Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm...
- Bài tập 5.Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của...
- Bài tập 6.Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có...
Bình luận (0)





