Bài tập 6. Một cái cổng hình bán nguyệt rọng 8,4m, cao 4,2m như Hình 5. Mặt đường dưới cổng được...
Câu hỏi:
Bài tập 6. Một cái cổng hình bán nguyệt rọng 8,4m, cao 4,2m như Hình 5. Mặt đường dưới cổng được chia thành hai làn xe ra vào.
a. Viết phương trình mô phỏng cái cổng.
b. Một chiếc xe tải rộng 2,2 m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng hay không?
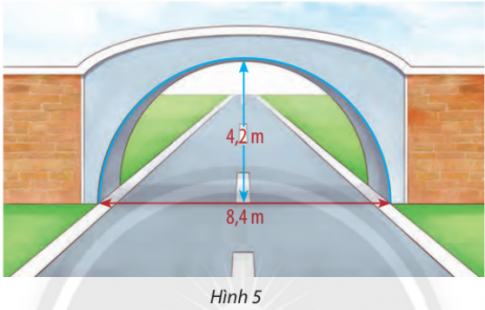
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Việt
a. Ta chọn hệ tọa độ Oxy như hình vẽ. Đường tròn có tâm O(0; 0) và bán kính R = 4,2 nên phương trình của đường tròn đó là $x^{2} + y^{2} = 17,64$. Phương trình mô phỏng cái cổng là $x^{2} + y^{2} = 17,64$ (y ≥ 0).b. Để xe tải đi qua cổng mà không làm hư hỏng cổng, ta cần kiểm tra xem chiều rộng và chiều cao của xe có nhỏ hơn chiều rộng và chiều cao của cổng không. Thay x = 2,2 vào phương trình đường tròn ta được: $y = \sqrt{17,64 - 2,2^{2}}$ ≈ 3,58 > 2,6. Vậy xe tải rộng 2,2m và cao 2,6m đi đúng làn đường quy định có thể đi qua cổng mà không làm hư hỏng cổng.
Câu hỏi liên quan:
- Bài tập 1. Phương trình nào trong các phương trình sau đây là phương trình đường tròn? Tìm tọa độ...
- Bài tập 2. Lập phương trình đường tròn (C) trong các trường hợp sau:a. (C) có tâm I(1; 5) và có bán...
- Bài tập 3. Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là:a. M(2; 5), N(1;...
- Bài tập 4. Lập phương trình đường tròn tiếp xúc với hai trục Ox, Oy và đi qua điểm A(4; 2).
- Bài tập 5. Cho đường tròn (C) có phương trình $x^{2} + y^{2} - 2x - 4y - 20 = 0$.a. Chứng tỏ rằng...






Do đó, khi xe tải có kích thước lớn hơn kích thước của cổng, xe tải sẽ không đi qua cổng mà không làm hư hỏng cổng.
Nếu xe tải vượt quá kích thước chiều rộng hoặc chiều cao của cổng, xe tải sẽ không thể đi qua cổng mà không làm hư hỏng cổng.
Để kiểm tra việc xe tải đi qua cổng mà không làm hư hỏng cổng, ta cần xem xét tọa độ và kích thước của xe tải so với cổng.
Để xe tải đi qua cổng mà không làm hư hỏng cổng, ta cần kiểm tra xem có thỏa mãn điều kiện không. Đầu tiên, xe tải phải rộng hơn hoặc bằng 2;2m và cao hơn hoặc bằng 2,6m. Ngoài ra, xe tải cần di chuyển trên làn đường được quy định.
Phương trình mô phỏng cái cổng sẽ là: {(x-4.2)^2 + (y-4.2)^2 = (4.2)^2, 0 <= x <= 8.4, 0 <= y <= 4.2}