Bài tập 6.14. Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa...
Câu hỏi:
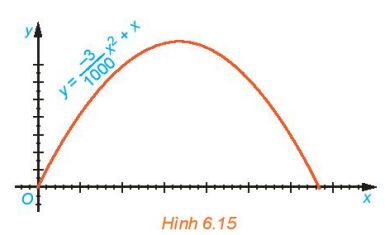
Bài tập 6.14. Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình $y=\frac{-3}{1000}x^{2}+x$, trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vật so với mặt đất
a. Tìm độ cao cực đại của vật trong quá trình bay.
b. Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Giang
Để tìm độ cao cực đại của vật trong quá trình bay, ta cần tìm tọa độ của đỉnh của parabol.
Để tìm Đỉnh của parabol có phương trình $y=ax^2+bx+c$ ta có công thức: $(x_{1};y_{1})=\left ( -\frac{b}{2a};-\frac{b^{2}-4ac}{4a} \right )$.
Áp dụng công thức trên và biến thể ta được tọa độ đỉnh của parabol $y=\frac{-3}{1000}x^{2}+x$ là $(\frac{500}{3};\frac{250}{3})$.
Do đó, độ cao cực đại của vật là $\frac{250}{3} \approx 83.3$ mét.
Để tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O, ta giải phương trình $y=\frac{-3}{1000}x^{2}+x=0$ để tìm nghiệm x.
Giải phương trình ta được $x_{1}=0$ và $x_{2}=\frac{1000}{3}$.
Điểm chạm đất sau khi bay của vật có tọa độ A($a,0$) với $a$ là số thực dương.
Từ đó, ta có $a=\frac{1000}{3}$.
Vậy, khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O là $\frac{1000}{3} \approx 333.3$ mét.
Để tìm Đỉnh của parabol có phương trình $y=ax^2+bx+c$ ta có công thức: $(x_{1};y_{1})=\left ( -\frac{b}{2a};-\frac{b^{2}-4ac}{4a} \right )$.
Áp dụng công thức trên và biến thể ta được tọa độ đỉnh của parabol $y=\frac{-3}{1000}x^{2}+x$ là $(\frac{500}{3};\frac{250}{3})$.
Do đó, độ cao cực đại của vật là $\frac{250}{3} \approx 83.3$ mét.
Để tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O, ta giải phương trình $y=\frac{-3}{1000}x^{2}+x=0$ để tìm nghiệm x.
Giải phương trình ta được $x_{1}=0$ và $x_{2}=\frac{1000}{3}$.
Điểm chạm đất sau khi bay của vật có tọa độ A($a,0$) với $a$ là số thực dương.
Từ đó, ta có $a=\frac{1000}{3}$.
Vậy, khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O là $\frac{1000}{3} \approx 333.3$ mét.
Câu hỏi liên quan:
- Bài tập 6.7. Vẽ các đường parabol sau:a. $y=x^{2}-3x+2$b. $y=-2x^{2}+2x+3$c. $y=x^{2}+2x+1$d....
- Bài tập 6.8. Từ các parabol đã vẽ ở Bài tập 6.7 hãy cho biết khoảng đồng biến và khoảng nghịch biến...
- Bài tập 6.9. Xác định parabol $y = ax^{2}+bx+1$. trong mỗi trường hợp sau:a. Đi qua hai điểm A(1; ...
- Bài tập 6.10. Xác định parabol $y = ax^{2}+bx+1$, biết rằng parabol đó đi qua điểm A(8; 0) và có...
- Bài tập 6.11. Gọi (P) là đồ thị hàm số bậc hai $y = ax^{2}+bx+1$. Hãy xác định dấu của hệ số a và...
- Bài tập 6.12. Hai bạn An và Bình trao đổi với nhau:An nói: Tớ đọc ở một tài liệu thấy nói rằng cổng...
- Bài tập 6.13. Bác Hùng dùng 40 m lưới thép gai rào thành một mảnh vườn hình chữ nhật để trồng...






Sau khi tính được độ cao cực đại và tầm xa của quỹ đạo, ta sẽ có thông tin cụ thể về hành trình bay của vật từ khi được ném lên đến khi chạm đất đồng thời đạt được kiến thức và kỹ năng giải quyết bài toán vật lý liên quan đến parabol.
Để tính tầm xa của quỹ đạo, ta cần tìm điểm chạm của parabol với trục Ox, tức là tìm điểm mà y=0. Khi đã xác định được x-coordinate của điểm chạm đất, ta tính được khoảng cách từ điểm chạm đất đến gốc O là khoảng cách này chính là tầm xa của quỹ đạo.
Sau khi tìm được đạo hàm của phương trình, ta giải phương trình f'(x)=0 để tìm vị trí điểm đỉnh. Khi đã xác định được x-coordinate của điểm đỉnh, ta thay giá trị này vào phương trình ban đầu để tính được độ cao cực đại.
Để tìm độ cao cực đại của vật trong quá trình bay, ta cần tìm điểm đỉnh của parabol. Để làm điều này, ta thực hiện việc đạo hàm của phương trình y=x(- rac{3}{1000}x+1).