Bài tập 4.27 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT:Bác Mến muốn tính khoảng...
Câu hỏi:
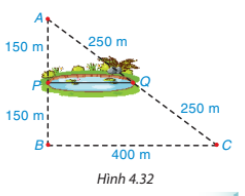
Bài tập 4.27 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Bác Mến muốn tính khoảng cách giữa hai vị trí P và Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.32. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hưng
Để tính khoảng cách giữa hai điểm P và Q, ta sử dụng phương pháp vế tựa vào tính chất đường trung bình trong tam giác.Đầu tiên, ta có AP = PB, do đó P là trung điểm của đoạn thẳng AB.Tương tự, ta có AQ = QC, suy ra Q là trung điểm của đoạn thẳng AC.Vậy, ta có PQ là đường trung bình của tam giác ABC.Do đó, ta có PQ = 1/2 BC = 1/2 * 400 = 200 (m).Vậy, khoảng cách giữa hai điểm P và Q là 200 mét.
Câu hỏi liên quan:
- A. Trắc nghiệmBài tập 4.18 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT:Độ dài x trong...
- Bài tập 4.19 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC. Gọi H, K lần...
- Bài tập 4.20 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC có chu vi là 32...
- Bài tập 4.21 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC có AB = 9 cm, D...
- Bài tập 4.22 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC cân tại A có AB...
- B. Tự luậnBài tập 4.23 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho góc xOy. Trên tia...
- Bài tập 4.24 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC vuông tại A. Gọi...
- Bài tập 4.25 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC, các đường trung...
- Bài tập 4.26 trang 89 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC, Điểm I thuộc...






Ngoài ra, để tính khoảng cách giữa hai vị trí P và Q trong không gian 2 chiều, ta cũng có thể sử dụng công thức hình học: d = sqrt((x2 - x1)^2 + (y2 - y1)^2), với (x1, y1) và (x2, y2) là tọa độ của hai điểm cần tính khoảng cách. Công thức này là công thức cơ bản và dễ áp dụng.
Một cách khác để tính khoảng cách giữa hai điểm P và Q là sử dụng định lí Pythagore. Theo định lí Pythagore, trong tam giác vuông ABC với AB là cạnh huyền và AC, BC là các cạnh góc vuông, ta có công thức: AB^2 = AC^2 + BC^2. Áp dụng vào trường hợp này, ta có thể tính khoảng cách giữa P và Q dựa trên ba điểm A, B, C đã cho.
Để tính khoảng cách giữa hai vị trí P và Q, ta có thể sử dụng công thức khoảng cách giữa hai điểm trong không gian 2 chiều: d = sqrt((x2 - x1)^2 + (y2 - y1)^2), trong đó P(x1, y1) và Q(x2, y2) là tọa độ của hai điểm cần tính khoảng cách.