Bài tập 10 trang 56 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính thể tích khối rubik có dạng...
Câu hỏi:
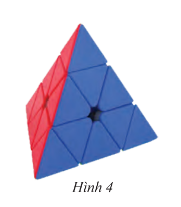
Bài tập 10 trang 56 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính thể tích khối rubik có dạng hình chóp tam giác đều (Hình 4). Biết khối rubik này có bốn mặt là tam giác đều bằng nhau cạnh 4.7 cm và chiều cao 4.1 cm, chiều cao của khối rubik bằng 3.9 cm
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Đạt
Để tính thể tích khối rubik có dạng hình chóp tam giác đều, ta cần sử dụng công thức tính thể tích của hình chóp tam giác đều: $V = \frac{1}{3}S_{đáy}h$. Trong trường hợp này, khối rubik có dạng hình chóp tam giác đều với bốn mặt tam giác đều có cạnh bằng 4.7 cm và chiều cao của chóp là 4.1 cm.Đầu tiên, ta cần tính diện tích đáy của khối rubik. Với tam giác đều, diện tích đáy được tính bằng công thức $S_{đáy} = \frac{1}{2}a \times h$, trong đó $a$ là cạnh của tam giác và $h$ là chiều cao của tam giác. Thay vào công thức ta có $S_{đáy} = \frac{1}{2} \times 4.7 \times 4.1 = 9.585 cm^{2}$.Sau đó, ta sử dụng công thức tính thể tích hình chóp tam giác đều: $V = \frac{1}{3} \times S_{đáy} \times h = \frac{1}{3} \times 9.585 \times 3.9 = 12.5255 cm^{3}$.Vậy, thể tích của khối rubik là 12.5255 $cm^{3}$.
Câu hỏi liên quan:
- Câu hỏi trắc nghiệmBài tập 1 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các phát...
- Bài tập 2 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các phát biểu sau, phát biểu...
- Bài tập 3 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các phát biểu sau, phát biểu...
- Bài tập 4 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: HÌnh chóp tam giác đều có diện tích...
- Bài tập 5 trang 54 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Hình chóp tứ giác đều có diện tích...
- Bài tập tự luậnBài tập 6 trang 55 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các tấm...
- Bài tập 7 trang 55 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Quan sát hình chóp tam giác đều ở...
- Bài tập 8 trang 55 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Quan sát hình chóp tứ giác đều ở...
- Bài tập 9 trang 55 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính diện tích xung quanh, diện tích...
- Bài tập 11 trang 56 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Lớp bạn Na dự định gấp 100 hộp đựng...
- Bài tập 12 trang 56 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một bể kính hình hộp chữ nhật chứa...






Đáp án cuối cùng là thể tích của khối rubik có dạng hình chóp tam giác đều là 25.6959 cm^3.
Như vậy, thể tích của khối rubik là 25.6959 cm^3.
Thay vào công thức thể tích V = 1/3 * S * h, ta có V = 1/3 * ((1/2) * 4.7^2 * √3) * 4.1 = 25.6959 cm^3.
Đối với khối rubik trong câu hỏi, diện tích đáy của hình chóp tam giác đều là S = (1/2) * a^2 * √3, với a là cạnh của tam giác đều.
Thể tích khối rubik có dạng hình chóp tam giác đều được tính bằng công thức V = 1/3 * (Diện tích đáy) * (Chiều cao).