Bài 2 trang 103 toán lớp 7 tập 2 CDTrong hình 95 đường thẳng a là đường trung trực của cả hai...
Câu hỏi:
Bài 2 trang 103 toán lớp 7 tập 2 CD
Trong hình 95 đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD. Chứng minh:
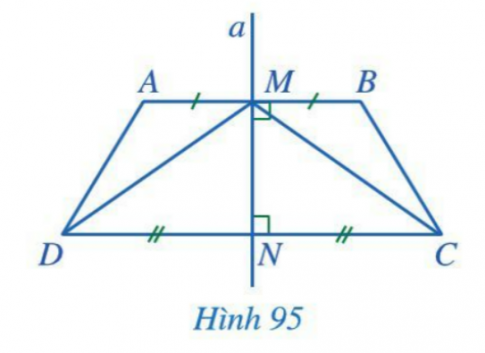
a. AB // CD
b. $\Delta MNC = \Delta MND$
c. $\widehat{AMD} = \widehat{BMC}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Phương
Để chứng minh các điều cần phải chứng minh trong bài toán trên, ta thực hiện các bước sau:
a. Vì đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD, nên ta có a vuông góc với cả hai đoạn thẳng AB và CD. Từ đó suy ra AB // CD.
b. Ta có $\Delta MNC$ và $\Delta MND$ có MN là cạnh chung, $\widehat{MNC} = \widehat{MND} = 90^\circ$ và DN = NC. Do đó, theo nguyên lý cạnh-góc-cạnh, ta có $\Delta MNC = \Delta MND$.
c. Vì AB // CD (theo câu a), ta có $\widehat{AMD} = \widehat{MDC}$. Từ $\Delta MNC = \Delta MND$, ta suy ra $\widehat{MDC} = \widehat{MCD}$. Cuối cùng, từ $\widehat{MCD} = \widehat{BMC}$ (vì a là đường trung trực của CD) suy ra $\widehat{AMD} = \widehat{BMC}$.
Vậy, các điều cần phải chứng minh đã được chứng minh.
a. Vì đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD, nên ta có a vuông góc với cả hai đoạn thẳng AB và CD. Từ đó suy ra AB // CD.
b. Ta có $\Delta MNC$ và $\Delta MND$ có MN là cạnh chung, $\widehat{MNC} = \widehat{MND} = 90^\circ$ và DN = NC. Do đó, theo nguyên lý cạnh-góc-cạnh, ta có $\Delta MNC = \Delta MND$.
c. Vì AB // CD (theo câu a), ta có $\widehat{AMD} = \widehat{MDC}$. Từ $\Delta MNC = \Delta MND$, ta suy ra $\widehat{MDC} = \widehat{MCD}$. Cuối cùng, từ $\widehat{MCD} = \widehat{BMC}$ (vì a là đường trung trực của CD) suy ra $\widehat{AMD} = \widehat{BMC}$.
Vậy, các điều cần phải chứng minh đã được chứng minh.
Câu hỏi liên quan:
- Bài 1 trang 103 toán lớp 7 tập 2 CDTrong hình 94, đường thẳng CD là đường trung trực của đoạn thẳng...
- Bài 3 trang 103 toán lớp 7 tập 2 CDCho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C....
- Bài 4 trang 103 toán lớp 7 tập 2 CDCho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M...






{
"content1": "Để chứng minh AB // CD, ta cần sử dụng tính chất của đường trung trực, tức là đường trung trực của một đoạn thẳng sẽ là đường vuông góc với đoạn thẳng đó. Do đó, ta cần chứng minh đường thẳng a là đường vuông góc với hai đoạn thẳng AB và CD.",
"content2": "Để chứng minh $\Delta MNC = \Delta MND$, ta cần sử dụng hai tam giác có cạnh và góc đồng đều. Trong trường hợp này, ta có hai tam giác MNC và MND cùng có cạnh MN và đồng thời góc M cũng bằng nhau do đường a là đường trung trực của AB và CD.",
"content3": "Để chứng minh $\widehat{AMD} = \widehat{BMC}$, ta cũng sử dụng tính chất của đường trung trực. Do đường a là đường trung trực của AB và CD, ta có $\widehat{AMD} = \widehat{DMC}$ và $\widehat{BMC} = \widehat{DMC}$. Từ đó suy ra $\widehat{AMD} = \widehat{BMC}$.",
"content4": "Chứng minh AB // CD: Gọi I là giao điểm của AB và CD. Ta có AI = IC (vì a là đường trung trực của AB và CD) và AI = IB (cùng chung góc MIA). Từ đó suy ra AB // CD.",
"content5": "Chứng minh $\Delta MNC = \Delta MND$: Ta có MN // CD (do a là đường trung trực của CD), từ đó suy ra $\Delta MNC = \Delta MND$ (do cạnh đối với hai góc bằng nhau).",
"content6": "Chứng minh $\widehat{AMD} = \widehat{BMC}$: Ta có AI // BM (do a là đường trung trực của AB) và MC // BI (do a là đường trung trực của CD). Từ đó suy ra $\widehat{AMD} = \widehat{BMC}$ (vì cùng là các góc so le)."
}