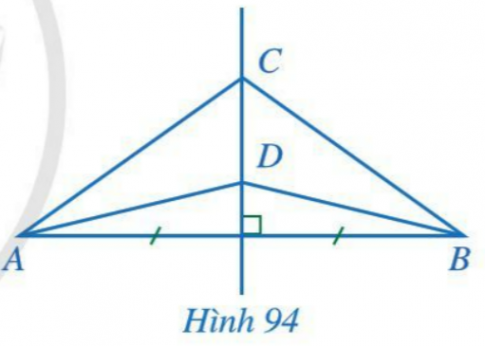
Bài 1 trang 103 toán lớp 7 tập 2 CDTrong hình 94, đường thẳng CD là đường trung trực của đoạn thẳng...
Câu hỏi:
Bài 1 trang 103 toán lớp 7 tập 2 CD
Trong hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh $\widehat{CAD} = \widehat{CBD}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Huy
Để chứng minh $\widehat{CAD} = \widehat{CBD}$, ta có thể làm như sau:1. Vì CD là đường trung trực của AB, nên ta có $CD \perp AB$.2. Gọi H là giao điểm của CD và AB.3. Xét tam giác DHA và tam giác DHB:- DH chung- $\widehat{DHA} = \widehat{DHB} = 90^{\circ}$- AH = HB=> Tứ giác DHAH là hình thoi=> $\Delta DHA = \Delta DHB$=> $\widehat{DAH} = \widehat{DBH}$ (1)4. Chứng minh tương tự với tam giác AHC và tam giác BHC:- AH chung- $\widehat{AHC} = \widehat{BHC} = 90^{\circ}$- HC = HC=> $\Delta AHC = \Delta BHC$=> $\widehat{CAH} = \widehat{CBH}$ (2)5. Từ (1) và (2) suy ra $\widehat{CAD} = \widehat{CBD}$.Vậy, chúng ta đã chứng minh được $\widehat{CAD} = \widehat{CBD}$.
Câu hỏi liên quan:
- Bài 2 trang 103 toán lớp 7 tập 2 CDTrong hình 95 đường thẳng a là đường trung trực của cả hai...
- Bài 3 trang 103 toán lớp 7 tập 2 CDCho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C....
- Bài 4 trang 103 toán lớp 7 tập 2 CDCho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M...






{ "content1": "Để chứng minh $\widehat{CAD} = \widehat{CBD}$, ta cần sử dụng tính chất của đường trung trực trong tam giác.", "content2": "Ta có đường thẳng CD là đường trung trực của đoạn thẳng AB nên $\widehat{CAD} = \widehat{ACD}$ và $\widehat{CBD} = \widehat{BCD}$.", "content3": "Từ đó ta có $\widehat{CAD} = \widehat{ACD} = \widehat{BCD} = \widehat{CBD}$ do $\widehat{ACD}$ và $\widehat{BCD}$ là cặp góc so le.", "content4": "Như vậy, ta đã chứng minh được $\widehat{CAD} = \widehat{CBD}$.", "content5": "Vậy nên, câu trả lời cho câu hỏi trên là $\widehat{CAD} = \widehat{CBD}$."}