4.50.Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường...
Câu hỏi:
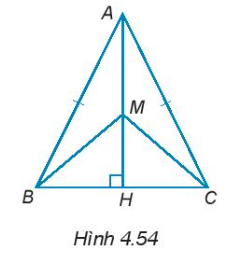
4.50. Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường thẳng AH sao cho M không trùng với A (H.4.54). Chứng minh rằng: $\widehat{MBA}=\widehat{MCA}$
Câu trả lời:
Người trả lời: GV. Đỗ Văn Linh
Phương pháp giải:Ta chứng minh rằng $\widehat{MBA}=\widehat{MCA}$ bằng cách sử dụng định lí cơ bản về hai tam giác đồng dạng.Gọi $D$ là hình chiếu từ $M$ đến $BC$. Khi đó, ta có $\Delta ABM \sim \Delta ACD$ (theo góc).Vì tam giác $ABC$ cân tại đỉnh $A$, nên ta có $AB = AC$.Do đó, $\Delta ABM \sim \Delta ACD$ có $AB = AC$ và $\widehat{BAM} = \widehat{CAD}$.Kết hợp với $\widehat{BAM} = \widehat{CAM}$ (do $M$ trên đường cao $AH$), ta suy ra $\widehat{MBA} = \widehat{MCA}$.Vậy, đã chứng minh được $\widehat{MBA} = \widehat{MCA}$.Câu trả lời: $\widehat{MBA} = \widehat{MCA}$.
Câu hỏi liên quan:
- BÀI TẬP4.41.Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại...
- 4.42.Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).
- 4.43.Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC...
- 4.44.Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia...
- 4.45.Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:a) Hai đường trung tuyến BM, CN...
- 4.46.Cho các điểm A, B, C, D, E như hình 4.51. Chứng minh rằng:a) $\Delta AEB$ và $\Delta...
- 4.47.Cho tam giác ABH vuông tại đỉnh H có $\widehat{ABH}=60^{\circ}$. Trên tia đối của tia HB...
- 4.48.Đường thẳng d trong hình nào dưới đây là trung trực của đoạn thẳng AB?
- 4.49.Cho A là một điểm tùy ý nằm trên đường trung trực của đoạn thẳng BC sao cho A...
Bình luận (0)





