4.43.Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC...
Câu hỏi:
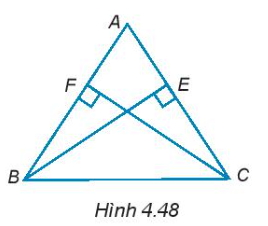
4.43. Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC cân tại đỉnh A.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ngọc
Để chứng minh rằng tam giác ABC cân tại đỉnh A, ta có thể giải bằng các bước sau:Bước 1: Gọi H là giao điểm của hai đường cao BE và CF.Bước 2: Ta có $\Delta ABE$ và $\Delta ACF$ là hai tam giác vuông tại E và F, từ đó suy ra $\widehat{ABE} = 90^\circ - \widehat{A}$ và $\widehat{ACF} = 90^\circ - \widehat{A}$.Bước 3: Khi đó, ta có $\widehat{ABE} = \widehat{ACF}$.Bước 4: Do BE = CF (theo giả thiết) và $\widehat{ABE} = \widehat{ACF}$, ta có $\Delta ABE = \Delta ACF$ (theo góc - cạnh - góc).Bước 5: Từ đó, ta suy ra AB = AC (hai cạnh tương ứng).Bước 6: Như vậy, tam giác ABC cân tại đỉnh A.Vậy câu trả lời cho câu hỏi "Tam giác ABC có hai đường cao BE và CF bằng nhau. Chứng minh rằng tam giác ABC cân tại đỉnh A" là tam giác ABC cân tại đỉnh A.
Câu hỏi liên quan:
- BÀI TẬP4.41.Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại...
- 4.42.Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).
- 4.44.Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia...
- 4.45.Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:a) Hai đường trung tuyến BM, CN...
- 4.46.Cho các điểm A, B, C, D, E như hình 4.51. Chứng minh rằng:a) $\Delta AEB$ và $\Delta...
- 4.47.Cho tam giác ABH vuông tại đỉnh H có $\widehat{ABH}=60^{\circ}$. Trên tia đối của tia HB...
- 4.48.Đường thẳng d trong hình nào dưới đây là trung trực của đoạn thẳng AB?
- 4.49.Cho A là một điểm tùy ý nằm trên đường trung trực của đoạn thẳng BC sao cho A...
- 4.50.Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường...






Khi BE = CF và ta kẻ đường thẳng qua O song song với AB và cắt AC tại D, suy ra tam giác AOB và tam giác AOC đều. Từ đó suy ra tam giác ABC cân tại đỉnh A.
Suy ra tam giác BOC đều, từ đó ta suy ra tam giác ABC cân tại đỉnh A.
Đặt O là trung điểm của đoạn thẳng BC. Khi đó, ta có BO = CO và góc BOC = 90 độ (vì đường cao BE và CF vuông góc với BC).
Khi đó, ta có góc ABC = góc ACB (do tam giác đối xứng có hai góc bằng nhau), suy ra tam giác ABC cân tại đỉnh A.
Ta có BE = CF (đường cao của tam giác ABC), suy ra tam giác ABC đối xứng qua đường trục BE.