4.42.Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).
Câu hỏi:
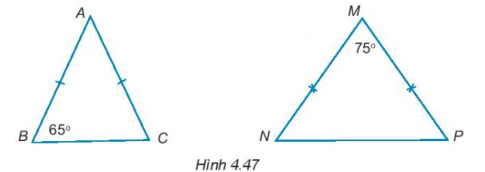
4.42. Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).
Câu trả lời:
Người trả lời: GV. Đỗ Văn Phương
Để tính số đo các góc còn lại trong các tam giác cân, ta cần áp dụng định lí tổng ba góc trong tam giác.Phương pháp giải:1. Với tam giác cân ABC:- Vì AB = AC, nên tam giác ABC cân tại đỉnh A.- Ta có $\widehat{C}=\widehat{B}=65^{\circ}$.- Áp dụng định lí tổng ba góc trong tam giác ABC, ta có $\widehat{A}=180-(\widehat{B}+\widehat{C})=180^{\circ}-(65^{\circ}+65^{\circ})=50^{\circ}$.2. Với tam giác cân MNP:- Vì MN = MP, nên tam giác MNP cân tại đỉnh M.- Ta có $\widehat{P}=\widehat{N}$.- Áp dụng định lí tổng ba góc trong tam giác MNP, ta có $2\widehat{N}=180^{\circ}-\widehat{M}=180^{\circ}-75^{\circ}=105^{\circ}$.- Vậy $\widehat{N}=52.5^{\circ}$, suy ra $\widehat{P}=\widehat{N}=52.5^{\circ}$.Câu trả lời:- Trong tam giác ABC: $\widehat{A}=50^{\circ}$, $\widehat{B}=65^{\circ}$, $\widehat{C}=65^{\circ}$.- Trong tam giác MNP: $\widehat{M}=75^{\circ}$, $\widehat{N}=52.5^{\circ}$, $\widehat{P}=52.5^{\circ}$.Vậy số đo các góc còn lại trong các tam giác cân là:- Trong tam giác ABC: $\widehat{A}=50^{\circ}$.- Trong tam giác MNP: $\widehat{M}=75^{\circ}$.
Câu hỏi liên quan:
- BÀI TẬP4.41.Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại...
- 4.43.Tam giác ABC có hai đường cao BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC...
- 4.44.Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia...
- 4.45.Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:a) Hai đường trung tuyến BM, CN...
- 4.46.Cho các điểm A, B, C, D, E như hình 4.51. Chứng minh rằng:a) $\Delta AEB$ và $\Delta...
- 4.47.Cho tam giác ABH vuông tại đỉnh H có $\widehat{ABH}=60^{\circ}$. Trên tia đối của tia HB...
- 4.48.Đường thẳng d trong hình nào dưới đây là trung trực của đoạn thẳng AB?
- 4.49.Cho A là một điểm tùy ý nằm trên đường trung trực của đoạn thẳng BC sao cho A...
- 4.50.Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tùy ý trên đường...






Đặt số đo của hai góc ở đỉnh của tam giác cân là x. Ta có tổng số đo của tam giác cân là 180°, nên ta có phương trình 2x + x = 180. Giải phương trình ta được x = 60°. Vậy số đo của các góc còn lại trong tam giác cân là 60°.
Gọi số đo của hai góc ở đỉnh của tam giác cân là x. Theo tính chất của tam giác cân, ta có: 2x + x = 180° (số đo của tam giác bằng 180°). Từ đó suy ra x = 60°. Vậy số đo của các góc còn lại trong tam giác cân là 60°.
Sử dụng công thức tổng số đo các góc trong tam giác là 180° để tính số đo các góc còn lại trong tam giác cân. Vì tam giác cân có 3 góc, nên tổng số đo các góc là 180° * 3 = 540°. Để tính số đo các góc còn lại, ta trừ đi số đo của hai góc ở đỉnh (60° + 60°) và được kết quả là 420°.
Với tam giác cân, ta biết rằng hai góc ở đỉnh đều bằng nhau. Ta có thể tính được số đo của mỗi góc là 180°/3 = 60°. Vậy số đo của các góc còn lại trong tam giác cân là 60°.