Bài tập 7 trang 60 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Cho ABCD là hình bình hành. Một...
Câu hỏi:
Bài tập 7 trang 60 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:
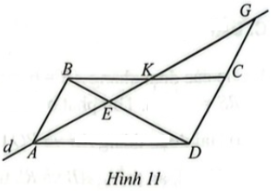
Cho ABCD là hình bình hành. Một đường thẳng d đi qua 4 cắt BD, BC, DC lần lượt tại E, K, G (Hình 11).
Chứng minh:
a) AE$^{2}$ = EK.EG;
b) $\frac{1}{AE}=\frac{1}{AK}=\frac{1}{AG}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Long
Phương pháp giải:a) Ta có AD // BK, AB // DG nên theo định lí Thalès, ta có $\frac{EK}{AE}=\frac{EB}{ED}=\frac{AE}{EG}$ hay $\frac{EK}{AE}=\frac{AE}{EG}$ => AE$^{2}$ = EK.EG.b) Ta có $\frac{AE}{AK}=\frac{DE}{DB}$ và $\frac{AE}{AG}=\frac{BE}{BD}$. Từ đó, ta có $\frac{AE}{AK}+\frac{AE}{AG}=\frac{DE}{DB}+\frac{BE}{BD}=\frac{BD}{BD} = 1$ => $AE.\left ( \frac{1}{AK}+\frac{1}{AG} \right )=1$. Vậy $\frac{1}{AE}=\frac{1}{AK}=\frac{1}{AG}$.Vậy đó là cách giải bài toán trên.
Câu hỏi liên quan:
- Bài tập 1 trang 59 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Cho các đoạn thẳng AB = 6 cm, CD =...
- Bài tập 2 trang 59 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Cho các đoạn thẳng EF = 6 cm, GH =...
- Bài tập 3 trang 59 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Cho tam giác ABC. Một đường thẳng...
- Bài tập 4 trang 60 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Toà nhà Bitexco Financial (hay...
- Bài tập 5 trang 60 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Cho tam giác ABC vuông ở A. Vẽ ra...
- Bài tập 6 trang 60 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Trong Hình 10, cho biết ABCD là...
- Bài tập 8 trang 60 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:An có một mảnh bìa có dạng hình...
- Bài tập 9 trang 60 sách bài tập (SBT) toán lớp 8 tập 2 cánh diều:Cho tam giác ABC có ba góc nhọn,...






Cách tiếp cận khác để chứng minh AE^2 = EK * EG và 1/AE = 1/AK = 1/AG là sử dụng định lý hình học về các tỷ số trong tam giác và đường chéo của hình bình hành.
Dựa vào định lí hình học về hình bình hành và tính chất của các góc trong hình bình hành, ta có thể chứng minh AE^2 = EK * EG và 1/AE = 1/AK = 1/AG.
Áp dụng định lí về tỷ lệ đối của các cạnh trong tam giác, ta có thể chứng minh rằng 1/AE = 1/AK = 1/AG.
Ta có thể sử dụng tính chất của hình bình hành và các đặc điểm của các góc trong hình bình hành để chứng minh AE^2 = EK * EG.
Để chứng minh 1/AE = 1/AK = 1/AG, ta có thể sử dụng định lí hình học về tỷ lệ đối của các đoạn thẳng trong tam giác. Có thể dùng công thức tính tỷ số của 3 đoạn thẳng trong tam giác để chứng minh điều này.