Bài tập 5.Cho 9 điểm nằm trên hai đường thẳng song song như Hình 3. Có bao nhiêu tam giác có...
Câu hỏi:
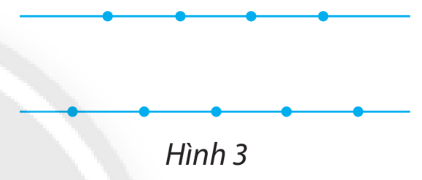
Bài tập 5. Cho 9 điểm nằm trên hai đường thẳng song song như Hình 3. Có bao nhiêu tam giác có các đỉnh là ba điểm trong các điểm đã cho?
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Linh
Để giải bài tập trên, chúng ta có thể làm theo hai cách sau:Cách 1:- Chọn 1 điểm trong 4 điểm nằm trên đường thẳng thứ nhất và chọn 2 điểm trong 5 điểm nằm trên đường thẳng thứ 2.- Số tam giác tạo thành là $C_{4}^{1} \times C_{5}^{2} = 4 \times 10 = 40$ tam giác.Cách 2:- Chọn 2 điểm trong 4 điểm nằm trên đường thẳng thứ nhất và chọn 1 điểm trong 5 điểm nằm trên đường thẳng thứ 2.- Số tam giác tạo thành là $C_{4}^{2} \times C_{5}^{1} = 6 \times 5 = 30$ tam giác.Áp dụng quy tắc cộng, tổng số tam giác có đỉnh trong các điểm đã cho là: 40 + 30 = 70 tam giác.Vậy, có tổng cộng 70 tam giác có các đỉnh là ba điểm trong 9 điểm đã cho.
Câu hỏi liên quan:
- Bài tập 3.Từ 6 thẻ số như Hình 2, có thể ghép để tạo thành bao nhiêua. Số tự nhiên có sáu chữ...
- Bài tập 4.Thực đơn tại một quán cơm văn phòng có 6 món mặn, 5 món rau và 3 món canh. Tại đây,...
- Bài tập 6.Khai triển các biểu thứca. ${{\left( a-\frac{b}{2} \right)}^{4}}$b....
- Bài tập 7.Hãy khai triển và rút gọn biểu thức${{(1+x)}^{4}}+{{(1-x)}^{4}}$Sử dụng kết quả đó...






Kết quả cuối cùng sẽ là số lượng tam giác có các đỉnh là ba điểm trong 9 điểm đã cho sau khi loại bỏ trường hợp các đỉnh thẳng hàng.
Số lượng tam giác có các đỉnh là ba điểm trong 9 điểm đã cho sẽ bằng số cách chọn 3 điểm từ tổng số điểm trừ đi số lượng tam giác có tất cả ba đỉnh trên cùng một đường thẳng.
Sau khi xác định được các điểm thẳng hàng, ta tính số lượng tam giác bằng cách chọn 3 điểm từ danh sách đã cho và kiểm tra xem có tạo thành một tam giác hay không.
Để tìm số lượng tam giác có các đỉnh là ba điểm trong 9 điểm đã cho, ta cần xác định các điểm thẳng hàng trên hai đường thẳng song song.