Bài tập 4.Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một...
Câu hỏi:
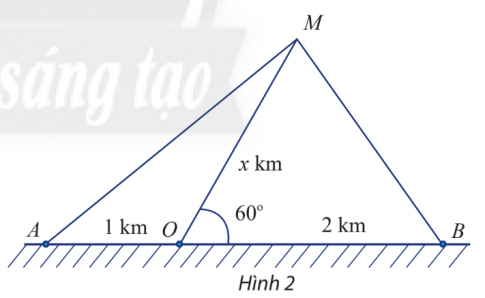
Bài tập 4. Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60°. Trên bờ biển có hai đài quan sát 4 và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng cách 1 km và 2 km (Hình 2).
a. Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.
b. Tìm x để khoảng cách từ tàu đến B bằng $\frac{4}{5}$ khoảng cách từ tàu đến A.
c. Tìm x để khoảng cách tử tàu đến B nhỏ hơn khoảng cách từ tàu đến O đảng 500 m. (Lưu ý: Làm tròn kết quả đến hàng phần trăm.)
Câu trả lời:
Người trả lời: GV. Đỗ Văn Ánh
a. Để biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x, ta cần áp dụng định lý cosin trong tam giác MOB và MOA như sau:Trong tam giác MOB:\( MB^2 = MO^2 + OB^2 - 2 \cdot MO \cdot OB \cdot \cos{60^\circ} \)\( MB^2 = x^2 + 2^2 - 2 \cdot x \cdot 2 \cdot \frac{1}{2} \)\( MB^2 = x^2 - 2x + 4 \)\( MB = \sqrt{x^2 - 2x + 4} \)Trong tam giác MOA:\( MA^2 = MO^2 + OA^2 - 2 \cdot MO \cdot OA \cdot \cos{120^\circ} \) (vì 180° - 60°)\( MA^2 = x^2 + 1^2 - 2 \cdot x \cdot 1 \cdot (-\frac{1}{2}) \)\( MA^2 = x^2 + x + 1 \)\( MA = \sqrt{x^2 + x + 1} \)b. Đề bài cho biết \( MB = \frac{4}{5} \cdot MA \), từ đó suy ra:\( \sqrt{x^2 - 2x + 4} = \frac{4}{5} \cdot \sqrt{x^2 + x + 1} \)\( x^2 - 2x + 4 = \frac{16}{25} \cdot (x^2 + x + 1) \)\( 9x^2 - 66x + 84 = 0 \)Giải phương trình trên ta được \( x \approx 5.7 \) hoặc \( x \approx 1.64 \)c. Để khoảng cách từ tàu đến B nhỏ hơn 500m so với khoảng cách từ tàu đến O, ta có:\( OM = MB + 0.5 \)\( x = \sqrt{x^2 - 2x + 4} + 0.5 \)\( x - 0.5 = \sqrt{x^2 - 2x + 4} \)\( x - 0.5 \) thỏa mãn yêu cầu khi \( x = 2.625 \)
Câu hỏi liên quan:






c. Để tìm x sao cho khoảng cách từ*** đến B nhỏ hơn khoảng cách từ*** đến O đảng 500 m, ta giải phương trình √(x² + 4) < x + 0.5. Sau khi giải phương trình ta được x ≈ 2.41 km.
b. Để tìm x sao cho khoảng cách từ*** đến B bằng $ rac{4}{5}$ khoảng cách từ*** đến A, ta giải phương trình √(x² + 4) = $ rac{4}{5}$√(x² + 1). Sau khi giải phương trình ta được x ≈ 2.44 km.
a. Để biểu diễn khoảng cách từ*** đến A và từ*** đến B theo x, ta sử dụng định lí Cosin trong tam giác MOA và MOB. Khoảng cách từ*** đến A là √(x² + 1) km và từ*** đến B là √(x² + 4) km.