Bài 40 : Giải các phương trình sau:
Câu hỏi:
Bài 40 : Giải các phương trình sau:
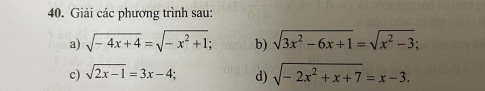
Câu trả lời:
Người trả lời: GV. Đỗ Văn Ngọc
Để giải các phương trình trong bài toán, chúng ta cần thực hiện các bước sau:Bước 1: Đưa các phương trình về dạng chuẩn, tức là một bên bằng 0.Bước 2: Xác định phương pháp giải phù hợp, có thể sử dụng công thức chuẩn hoặc phân tích từng trường hợp riêng biệt.Bước 3: Tính toán để tìm ra các nghiệm của phương trình.Câu trả lời chi tiết cho bài toán trên:Phương trình đã cho: a) x^2 - 2x - 3 = 0b) x^2 - 4x + 4 = 0c) 9x^2 - 34x + 27 = 0d) x^2 + 4x + 5 = 0a) Giải phương trình x^2 - 2x - 3 = 0:Đưa về dạng chuẩn: x^2 - 2x - 3 = 0Tìm các nghiệm của phương trình:(x - 3)(x + 1) = 0 => x = 3 hoặc x = -1Vậy phương trình có 2 nghiệm: x = 3 hoặc x = -1b) Giải phương trình x^2 - 4x + 4 = 0:Đưa về dạng chuẩn: x^2 - 4x + 4 = 0Tìm các nghiệm của phương trình:(x - 2)^2 = 0 => x = 2Vậy phương trình có 1 nghiệm duy nhất: x = 2c) Giải phương trình 9x^2 - 34x + 27 = 0:Đưa về dạng chuẩn: 9x^2 - 34x + 27 = 0Tìm các nghiệm của phương trình:(3x - 17)(3x - 9) = 0 => x = 17/9 hoặc x = 3Vậy phương trình có 2 nghiệm: x = 17/9 hoặc x = 3d) Giải phương trình x^2 + 4x + 5 = 0:Đưa về dạng chuẩn: x^2 + 4x + 5 = 0Tính delta: Δ = 4^2 - 4*1*5 = 16 - 20 = -4Vì delta < 0 nên phương trình vô nghiệm trong tập số thựcVậy phương trình không có nghiệm trong tập số thực. Kết luận: a) x = 3 hoặc x = -1b) x = 2c) x = 17/9 hoặc x = 3d) Phương trình vô nghiệm.
Câu hỏi liên quan:
- Bài 36 :Trong các phát biểu sau, phát biểu nào đúng?A. Tập nghiệm của phương...
- Bài 37 :Trong các phát biểu sau, phát biểu nào đúng?A. Tập nghiệm của phương...
- Bài 38 :Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = [g(x)]2thỏa...
- Bài 39 :Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình f(x) = [g(x)]2thỏa...
- Bài 41 :Giải các phương trình sau:
- Bài 42 :Để leo lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m. Ban...
- Bài 43 :Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc...
- Bài 44 :Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình...
Bình luận (0)





