Bài 1 trang 83 toán lớp 7 tập 2 CDCho Hình 42 có MN=QN; MP=QP. Chứng minh...
Câu hỏi:
Bài 1 trang 83 toán lớp 7 tập 2 CD
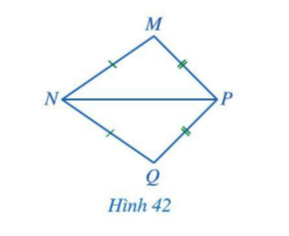
Cho Hình 42 có MN=QN; MP=QP. Chứng minh $\widehat{MNP}=\widehat{QNP}$
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Linh
Cách 1:Bước 1: Ta có MN=QN và MP=QP.Bước 2: Do MN=QN và MP=QP nên tam giác MNP và tam giác QNP là tam giác đều.Bước 3: Vì tam giác MNP và tam giác QNP là tam giác đều nên $\widehat{MNP}=\widehat{QNP}$.Vậy chúng ta đã chứng minh được $\widehat{MNP}=\widehat{QNP}$.Cách 2:Bước 1: Ta có MN=QN và MP=QP.Bước 2: Xét tam giác MNP và tam giác QNP.Bước 3: Ta có NP=NP (cạnh chung), MP=QP (đã cho), MN=QN (đã cho).Bước 4: Do NP=NP, MP=QP, MN=QN nên theo trường hợp đẳng cấp cạnh - cạnh - cạnh, ta có $\Delta MNP = \Delta QNP$.Bước 5: Vậy suy ra $\widehat{MNP}=\widehat{QNP}$.Vậy chúng ta đã chứng minh được $\widehat{MNP}=\widehat{QNP}$.
Câu hỏi liên quan:
- Bài 2 trang 83 toán lớp 7 tập 2 CDCho Hình 43 có AB=AD, $\widehat{ABC}=\widehat{ADC}=90^{0}$. Chứng...
- Bài 3 trang 83 toán lớp 7 tập 2 CDCho hình 44 có AC = BD, $\widehat{ABC} = \widehat{BAD} = 90^{0}$....
- Bài 4 trang 83 toán lớp 7 tập 2 CDCho hai tam giác ABC và MNP thỏa mãn: AB=MN, BC=NP, AC=MP,...






Khi đó ta suy ra góc MNP = góc QNP (do góc MNP + góc MON = 180 độ và góc QNP + góc POQ = 180 độ).
Do đó tam giác MNO và tam giác QPO đều có 2 cạnh bằng nhau nên góc MON = góc POQ (theo định lí cạnh và góc bằng nhau).
Ta có ON=OP (do MN=QN và MP=QP).
Gọi O là giao điểm của MN và QP.