3.17.Vẽ lại Hình 3.16 vào vở. Giải thích tại sao Hx // Ky
Câu hỏi:
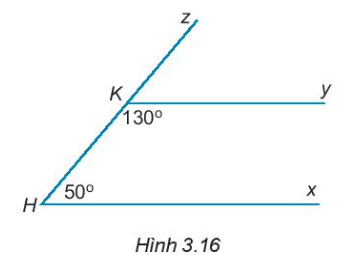
3.17. Vẽ lại Hình 3.16 vào vở. Giải thích tại sao Hx // Ky
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Hạnh
Để giải câu hỏi trên, ta thực hiện các bước sau:Bước 1: Vẽ lại Hình 3.16 vào vở.Bước 2: Ta có $\widehat{HKy} + \widehat{yKz} = 180^\circ$ (hai góc kề bù) hay $130^\circ + \widehat{yKz} = 180^\circ$. Do đó, $\widehat{yKz} = 180^\circ - 130^\circ = 50^\circ$.Bước 3: Ta có $\widehat{yKz} = \widehat{KHx} = 50^\circ$. Hai góc này ở vị trí đồng vị nên Ky // Hx (dấu hiệu nhân biết hai đường thẳng song song).Vậy câu trả lời đầy đủ là: Vì $\widehat{KHx} = \widehat{yKz}$ và đều bằng 50 độ, nên ta suy ra Ky // Hx.
Câu hỏi liên quan:
- BÀI TẬP3.9.Cho Hình 3.10.a) Viết tên góc so le trong với góc NMC.b) Viết tên góc đồng vị với...
- 3.10.Vẽ đường thẳng d và điểm M không thuộc d. Vẽ đường thẳng a đi qua M và song song với d.
- 3.11.Vẽ tam giác ABC bất kì. Vẽ đường thẳng xy đi qua điểm A và song song với BC.
- 3.12. Vẽ lại Hình 3.11 vào vở rồi giải thích vì sao xx'//yy'
- 3.13.Cho Hình 3.12. Giải thích tại sao a//b.
- 3.14.Cho Hình 3.13. Giải thích tại sao MN // PQ
- 3.15.Cho Hình 3.14. Giải thích tại sao EF // NP
- 3.16.Vẽ lại Hình 3.15 vào vở, biết NP//MQ và NP = MQ.






Ta có tam giác HBA và tam giác KBA cùng có cặp góc vuông tại B theo giả thiết, nên theo quy tắc về góc trong tam giác, ta suy ra Hx // Ky.
Do Hx cắt AB tạo góc vuông và Ky cũng cắt AB tạo góc vuông theo hình vẽ Hình 3.16, nên theo tính chất của đường thẳng song song và đường thẳng vuông góc, ta có Hx // Ky.
Hai đường thẳng Hx và Ky đều vuông góc với đường thẳng AB theo giả thiết của Hình 3.16, nên Hx // Ky do đường thẳng vuông góc với cùng một đường thẳng là song song với nhau.
Hình 3.16 cho biết Hx // AB và Ky // AB, vì hai đường thẳng đều song song với cùng một đường thẳng trên mặt phẳng nên Hx // Ky.