3.15.Cho Hình 3.14. Giải thích tại sao EF // NP
Câu hỏi:
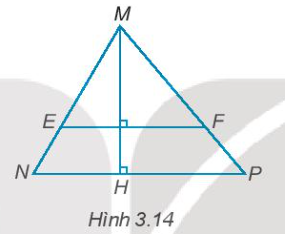
3.15. Cho Hình 3.14. Giải thích tại sao EF // NP
Câu trả lời:
Người trả lời: GV. Đỗ Văn Phương
Phương pháp giải:Giả sử ta kẹp góc MHF là x và góc MFN là y. Ta có: x + y = 90 (vì EF, NP là đường thẳng chéo của hình chữ nhật MHNP)Mặt khác:x = 90 - góc MHN (do góc thẳng trong)y = 90 - góc MNH (do góc thẳng trong)Mặt khác, ta có:góc MHN = góc NHF (cùng chắn cung NM trên đường tròn)góc MNH = góc MHN (do tam giác MNH đều)Từ đó suy ra:góc MHF = góc MFNNhư vậy, EF // NP (vì cặp góc đồng quy)Câu trả lời: Vậy, ta có $EF\perp MH,NP\perp MH$ nên EF // NP.
Câu hỏi liên quan:
- BÀI TẬP3.9.Cho Hình 3.10.a) Viết tên góc so le trong với góc NMC.b) Viết tên góc đồng vị với...
- 3.10.Vẽ đường thẳng d và điểm M không thuộc d. Vẽ đường thẳng a đi qua M và song song với d.
- 3.11.Vẽ tam giác ABC bất kì. Vẽ đường thẳng xy đi qua điểm A và song song với BC.
- 3.12. Vẽ lại Hình 3.11 vào vở rồi giải thích vì sao xx'//yy'
- 3.13.Cho Hình 3.12. Giải thích tại sao a//b.
- 3.14.Cho Hình 3.13. Giải thích tại sao MN // PQ
- 3.16.Vẽ lại Hình 3.15 vào vở, biết NP//MQ và NP = MQ.
- 3.17.Vẽ lại Hình 3.16 vào vở. Giải thích tại sao Hx // Ky






Từ tính chất của tỉ số đối với các đường thẳng song song, ta có EF // NP khi EF là đường phân giác trong tam giác EAF và NP là đường phân giác trong tam giác NPA.
EF // NP vì hai đường thẳng này đều song song với đường thẳng AB theo tính chất của các đường thẳng song song.
Khi EF // NP, ta có tỉ số của các cặp đường chéo trong tam giác EAF và tam giác NPA bằng nhau, do đó EF // NP.
Áp dụng định lí Euclid về tuyến tính, ta có EF // NP vì hai đường thẳng EF và NP cắt nhau tại một góc vuông.
Từ góc AEF = góc ENP và góc EF có cùng chung cạnh AF, ta suy ra EF // NP bằng tính chất của các góc cân.