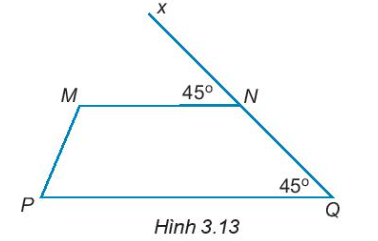
3.14.Cho Hình 3.13. Giải thích tại sao MN // PQ
Câu hỏi:
3.14. Cho Hình 3.13. Giải thích tại sao MN // PQ
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Long
Phương pháp giải:1. Góc MNx = Góc PQN (Do MNx và PQN là góc so le cân đối)2. Góc MNx = 45 độ (theo giả thiết)3. Góc PQN = 45 độ (Do 2 góc bằng nhau với góc cặp so le cân đối)4. Do góc PQN = 45 độ và góc PQN = 45 độ nên MN // PQ (theo tính chất của góc song song) Vậy ta đã chứng minh được MN // PQ.Câu trả lời: Ta có $\widehat{MNx}=\widehat{PQN}(=45^{\circ}).$Hai góc này ở vị trí đồng vị nên MN // PQ (dấu hiệu nhận biết hai đường thẳng song song).
Câu hỏi liên quan:
- BÀI TẬP3.9.Cho Hình 3.10.a) Viết tên góc so le trong với góc NMC.b) Viết tên góc đồng vị với...
- 3.10.Vẽ đường thẳng d và điểm M không thuộc d. Vẽ đường thẳng a đi qua M và song song với d.
- 3.11.Vẽ tam giác ABC bất kì. Vẽ đường thẳng xy đi qua điểm A và song song với BC.
- 3.12. Vẽ lại Hình 3.11 vào vở rồi giải thích vì sao xx'//yy'
- 3.13.Cho Hình 3.12. Giải thích tại sao a//b.
- 3.15.Cho Hình 3.14. Giải thích tại sao EF // NP
- 3.16.Vẽ lại Hình 3.15 vào vở, biết NP//MQ và NP = MQ.
- 3.17.Vẽ lại Hình 3.16 vào vở. Giải thích tại sao Hx // Ky






Qua việc so sánh các góc và cạnh của hai tam giác MNH và PQN, ta thấy chúng tương đồng nên có thể kết luận MN // PQ.
Sử dụng định lý trực giao, vì góc MHQ và NPQ bằng nhau (cùng bằng 90 độ), nên ta có MN // PQ.
Ta có thể sử dụng tính chất của tứ giác để giải thích: cả hai tam giác MNH và PQN đều là tam giác vuông cân, nên ta suy ra MN // PQ.
Theo tính chất của góc vuông, ta thấy góc MHQ và góc NPQ là góc vuông, từ đó suy ra đoạn MN song song với đoạn PQ.
Do hai góc MHQ và NPQ cùng bằng 90 độ (góc vuông), nên ta có cơ sở để kết luận rằng đoạn MN song song với đoạn PQ.