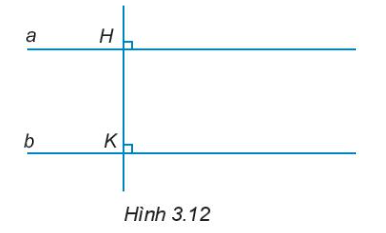
3.13.Cho Hình 3.12. Giải thích tại sao a//b.

Với bất kỳ hai đường thẳng nào song song với nhau, ta đều có a//b, đây chính là lý do vì sao a//b trong trường hợp này.

Áp dụng định lý tỉ lệ đồng đức, ta có hai đường thẳng a và b đồng quy tại một điểm nằm ở vô cùng. Từ đó suy ra a//b.

Do có một đường song song đi qua hai đường thẳng a và b, nên theo tính chất của các đường thẳng song song, ta có a//b.

Theo định lý của các góc, khi hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba, thì các góc tương ứng trong, tương quan ngoài và tương quan cùng chiều bằng nhau. Vì vậy, a//b.

Vì hai đường thẳng a và b có giá trị góc nội tiếp bằng nhau khi cắt bởi một đường song song, nên a//b.