19.Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở câu lạc bộ của Dũng (đường...
Câu hỏi:
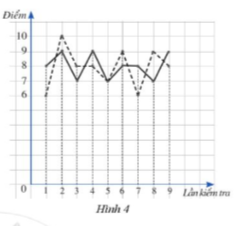
19. Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở câu lạc bộ của Dũng (đường nét liền) và Hoàng (đường nét đứt đậm) qua 9 lần kiểm tra.
a) Viết mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng và Hoàng nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mỗi mẫu số liệu đó.
c) Tính phương sai và độ lệch chuẩn của hai mẫu số liệu đó. Cho biết kết quả thi của bạn nào ổn định hơn?
Câu trả lời:
Người trả lời: GV. Đỗ Thị Dung
Để giải câu hỏi trên, ta thực hiện các bước như sau:
a) Mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng là: 8, 9, 7, 9, 7, 8, 8, 7, 9
Mẫu số liệu thống kê kết quả thi ngoại ngữ của Hoàng là: 6, 10, 8, 8, 7, 9, 6, 9, 8
b) Tính khoảng biến thiên và khoảng tứ phân vị:
- Đối với mẫu số liệu của Dũng:
Khoảng biến thiên R = 9 - 7 = 2
Khoảng tứ phân vị ∆Q = Q3 - Q1 = 9 - 7 = 2
- Đối với mẫu số liệu của Hoàng:
Khoảng biến thiên R = 10 - 6 = 4
Khoảng tứ phân vị ∆Q = Q3 - Q1 = 9 - 6.5 = 2.5
c) Tính phương sai và độ lệch chuẩn:
Phương sai của mẫu số liệu của Dũng: sD^2 = 2/3
Phương sai của mẫu số liệu của Hoàng: sH^2 = 134/81
Độ lệch chuẩn của mẫu số liệu của Dũng: sD = √(2/3)
Độ lệch chuẩn của mẫu số liệu của Hoàng: sH = √(134/81)
So sánh phương sai của hai mẫu số liệu, ta thấy phương sai của mẫu số liệu của Dũng nhỏ hơn phương sai của mẫu số liệu của Hoàng, vậy Dũng có kết quả thi ổn định hơn Hoàng.
a) Mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng là: 8, 9, 7, 9, 7, 8, 8, 7, 9
Mẫu số liệu thống kê kết quả thi ngoại ngữ của Hoàng là: 6, 10, 8, 8, 7, 9, 6, 9, 8
b) Tính khoảng biến thiên và khoảng tứ phân vị:
- Đối với mẫu số liệu của Dũng:
Khoảng biến thiên R = 9 - 7 = 2
Khoảng tứ phân vị ∆Q = Q3 - Q1 = 9 - 7 = 2
- Đối với mẫu số liệu của Hoàng:
Khoảng biến thiên R = 10 - 6 = 4
Khoảng tứ phân vị ∆Q = Q3 - Q1 = 9 - 6.5 = 2.5
c) Tính phương sai và độ lệch chuẩn:
Phương sai của mẫu số liệu của Dũng: sD^2 = 2/3
Phương sai của mẫu số liệu của Hoàng: sH^2 = 134/81
Độ lệch chuẩn của mẫu số liệu của Dũng: sD = √(2/3)
Độ lệch chuẩn của mẫu số liệu của Hoàng: sH = √(134/81)
So sánh phương sai của hai mẫu số liệu, ta thấy phương sai của mẫu số liệu của Dũng nhỏ hơn phương sai của mẫu số liệu của Hoàng, vậy Dũng có kết quả thi ổn định hơn Hoàng.
Câu hỏi liên quan:
- BÀI TẬP14.Cho mẫu số...
- 15.Biểu đồ đoạn thẳng ở Hình 2 biểu diễn thu nhập bình quân đầu người/năm của Việt Nam ở một...
- 16.Biểu đồ đoạn thẳng ở Hình 3 biểu diễn số lượt khách vào một cửa hàng trong ngày đầu khai...
- 17.Cho mẫu số...
- 18.Kết quả dự báo nhiệt độ cao nhất trong 10 ngày liên tiếp ở Nghệ An cuối tháng 01 năm 2022...
Bình luận (0)





