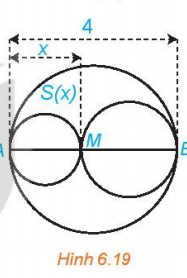
Bài tập 6.19. Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x....
Câu hỏi:
Bài tập 6.19. Xét đường tròn đường kính AB = 4 và một điểm M di chuyển trên đoạn AB, đặt AM = x. Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Phương
Để giải bài toán trên, ta cần xác định các giá trị của x sao cho diện tích S(x) không vượt qua một nửa tổng diện tích hai hình tròn nhỏ. Cách làm: 1. Xác định bán kính của hai hình tròn nhỏ sử dụng x và 4-x.2. Tính diện tích của hai hình tròn nhỏ.3. Tính diện tích phần nằm ngoài hai hình tròn nhỏ.4. Đặt điều kiện để diện tích S(x) không vượt qua một nửa tổng diện tích hai hình tròn nhỏ.Câu trả lời cho câu hỏi trên là: Để diện tích S(x) không vượt qua một nửa tổng diện tích hai hình tròn nhỏ, giá trị của x cần thỏa mãn điều kiện 0 < x ≤ 5.45.
Câu hỏi liên quan:
- Bài tập 6.15. Xét dấu các tam thức bậc hai sau:a. $3x^{2}-4x+1$b. $x^{2}+2x+1$c. $-x^{2}+3x-2$d....
- Bài tập 6.16. Giải các bất phương trình bậc hai:a. $x^{2}-1\geq 0$b. $x^{2}-2x-1<0$c....
- Bài tập 6.17. Tìm các giá trị của tham số m để tam thức bậc hai sau dương với mọi $x\in...
- Bài tập 6.18. Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 320 m với vận tốc ban...






Vậy kết luận, các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ là x thuộc đoạn [0, 1.22].
Để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ, ta cần thỏa mãn điều kiện 2x + 8-2x <= 2*(0.5*3.14*2^2), tức là x <= 1.22.
Diện tích tam giác OMB cũng là S2 = 2*(4-x) = 8-2x.
Ta có diện tích tam giác OAM là S1 = 0.5*x*4 = 2x.
Khi đó, diện tích S(x) nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ chính là diện tích tam giác OAM và tam giác OMB.