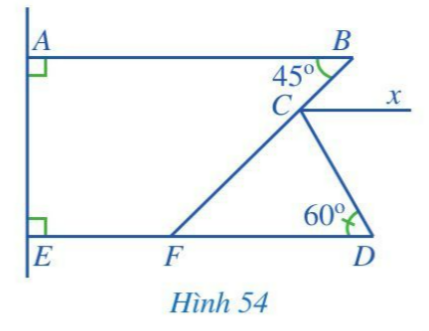
Bài 4 trang 108 toán lớp 7 tập 1 CDQuan sát hình 54, trong đó Cx song song với ABa. Chứng minh rằng...
Câu hỏi:
Bài 4 trang 108 toán lớp 7 tập 1 CD
Quan sát hình 54, trong đó Cx song song với AB
a. Chứng minh rằng Cx song song với DE
b. Chứng minh rằng $\widehat{BCx}=45^{0}$ và $\widehat{DCx}=60^{0}$
c. Tính $\widehat{BCD}$
Câu trả lời:
Người trả lời: GV. Đỗ Thị Huy
a) Vì AE vuông góc với AB và cũng vuông góc với ED nên ta có AB//ED. Vì Cx song song với AB, suy ra Cx cũng song song với ED.b) Vì Cx song song với AB nên góc ABC bằng góc BCx (do hai góc so le trong nhau). Với góc ABC bằng 45 độ, ta có góc BCx cũng bằng 45 độ. Tương tự, với Cx song song với ED, ta suy ra góc DCx bằng 60 độ.c) Vì tia Ox nằm trong góc BCD, ta có góc BCD bằng tổng của góc BCx và góc DCx, tức là 45 độ + 60 độ = 105 độ.Vậy kết quả là góc BCD bằng 105 độ.
Câu hỏi liên quan:






{ "content1": "Để chứng minh Cx song song với DE, ta có hai góc nhọn tương ứng và cùng chiều, nên theo tính chất góc đồng quy ta suy ra Cx song song với DE.", "content2": "Chứng minh $\widehat{BCx}=45^{0}$: Ta có góc ngoài tam giác ABC bằng tổng hai góc trong ABC nên $\widehat{ACB} = 135^{0}$. Vì AD song song với BC nên $\widehat{DCx} = \widehat{ACB} = 135^{0}$. Suy ra $\widehat{BCx} = 180^{0} - \widehat{ACB} = 180^{0} - 135^{0} = 45^{0}$.", "content3": "Chứng minh $\widehat{DCx}=60^{0}$: Tương tự, góc ngoài tam giác CDE bằng tổng hai góc trong nên $\widehat{CDE} = 180^{0} - 45^{0} = 135^{0}$. Vì AD song song với BC nên $\widehat{CDE} = \widehat{DCx} = 135^{0}$. Suy ra $\widehat{DCx} = 60^{0}$.", "content4": "Suy ra $\widehat{BCD}=180^{0} - \widehat{BCx} - \widehat{DCx} = 180^{0} - 45^{0} - 60^{0} = 75^{0}$.", "content5": "Vậy $\widehat{BCD}=75^{0}$."}