Bài 3 trang 108 toán lớp 7 tập 1 CDTìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d...
Câu hỏi:
Bài 3 trang 108 toán lớp 7 tập 1 CD
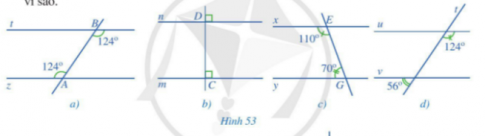
Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Việt
Cách làm:a) Ta thấy $\widehat{A_{1}} = \widehat{B_{1}} = 124^\circ$, và 2 góc này ở vị trí so le trong nên hai đường thẳng $AB$ và $CD$ là song song.b) Giả sử $\widehat{D_{1}}$ chính là $\widehat{D_{1}}$, ta có $\widehat{D_{1}} + \widehat{D_{2}} = 180^\circ$ (do 2 góc kề bù). Từ đó, ta có $\widehat{D_{2}} = 90^\circ$. Và vì $\widehat{D_{2}} = \widehat{C_{1}} = 90^\circ$, nên hai đường thẳng $CD$ và $EF$ là song song.c) Tương tự như trên, ta có $\widehat{E_{2}} = 70^\circ$ và $\widehat{E_{2}} = \widehat{G_{1}} = 70^\circ$, nên hai đường thẳng $EF$ và $GH$ là song song.d) Giả sử $\widehat{K_{1}}$ chính là $\widehat{K_{1}}$, ta có $\widehat{K_{1}} + 56^\circ = 180^\circ$, suy ra $\widehat{K_{1}} = 124^\circ$. Và vì $\widehat{H_{1}} = \widehat{K_{1}} = 124^\circ$, nên hai đường thẳng $HI$ và $JK$ là song song.Câu trả lời:a) Đường thẳng $AB$ và $CD$ là song song vì $\widehat{A_{1}} = \widehat{B_{1}} = 124^\circ$.b) Đường thẳng $CD$ và $EF$ là song song vì $\widehat{D_{1}} + \widehat{D_{2}} = 180^\circ$ và $\widehat{D_{2}} = \widehat{C_{1}} = 90^\circ$.c) Đường thẳng $EF$ và $GH$ là song song vì $\widehat{E_{1}} + \widehat{E_{2}} = 180^\circ$ và $\widehat{E_{2}} = \widehat{G_{1}} = 70^\circ$.d) Đường thẳng $HI$ và $JK$ là song song vì $\widehat{K_{1}} + 56^\circ = 180^\circ$ và $\widehat{H_{1}} = \widehat{K_{1}} = 124^\circ$.
Câu hỏi liên quan:






Trong hình 53c, cặp đường thẳng IJ và KL là song song vì chúng cắt nhau bởi một đường thẳng nên mỗi góc tạo bởi chúng là bằng nhau.
Trong hình 53b, cặp đường thẳng EF và GH là hai đường thẳng song song vì chúng có cùng một góc chịu và không gặp nhau.
Trong hình 53a, cặp đường thẳng AB và CD là đồng quy nên chúng là hai đường thẳng song song vì có dạng giống nhau và không bao giờ cắt nhau.