Bài 2 trang 86 toán lớp 7 tập 2 CDCho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc...
Câu hỏi:
Bài 2 trang 86 toán lớp 7 tập 2 CD
Cho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc vuông. Chứng minh:
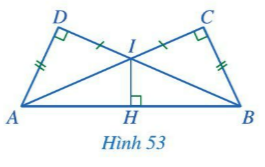
a. IA = IB
b. IH là tia phân giác của góc AIB
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Phương
Để chứng minh hai điều kiện trên, ta thực hiện các bước sau:a. Ta có $\Delta ADI$ và $\Delta ICB$ đều có một cạnh chung là $ID = IC$, hai cạnh tương ứng bằng nhau $AD = BC$ và góc vuông tại đỉnh $\widehat{D} = \widehat{C} = 90^{0}$. Do đó, theo nguyên lý công thức 3 góc của tam giác, ta có $\Delta ADB \cong \Delta ACB$, từ đó suy ra $IA = IB$.b. Xét $\Delta AIH$ và $\Delta BIH$, ta thấy chúng đều có cạnh chung $IH$, $I\widehat{HB} = I\widehat{HD} = 90^{0}$, và vì $IA = IB$ (do bước a), nên ta có thể kết luận $\Delta AIH = \Delta BIH$. Từ đó, ta có $\widehat{AIH} = \widehat{BIH}$, tức là $IH$ là tia phân giác của góc $AIB$.Vậy, câu trả lời đầy đủ và chi tiết cho câu hỏi trên là:a. $IA = IB$b. $IH$ là tia phân giác của góc $AIB$.Bạn vui lòng kiểm tra và thực hiện đúng theo hướng dẫn trên để hoàn thành bài toán.
Câu hỏi liên quan:






Từ đó suy ra tam giác ICD đều, suy ra IA = IB (do đường cao cùng cạnh huyền trong tam giác đều).
Vì IC = ID, góc ICD = góc IDC (ro ren).
Ta có IC = ID (theo điều kiện trong bài toán).