B - BÀI TẬP3.33.Cho Hình 3.33. Hãy chứng minh xy//x'y'
Câu hỏi:
B - BÀI TẬP
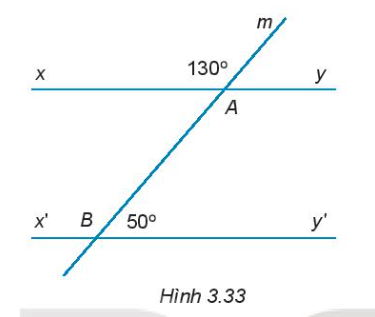
3.33. Cho Hình 3.33. Hãy chứng minh xy//x'y'
Câu trả lời:
Người trả lời: GV. Đỗ Thị Đức
Phương pháp giải:Ta có góc xAm kề bù với góc mAy nên $\widehat{mAy}=180^{\circ}-\widehat{xAm}=50^{\circ}$. Suy ra $\widehat{mAy}=\widehat{ABy'}$ (cùng bằng $50^{\circ}$) mà hai góc này ở vị trí đồng vị nên xy//xy'Vậy, chúng ta đã chứng minh được xy//xy'Hoặc phương pháp giải khác:Vì $\widehat{xAm}=\widehat{AmC}$ và $\widehat{mAy}=\widehat{Ay'C}$ (cùng bằng $130^{\circ}$). Do đó tam giác xAm đồng dạng với tam giác mAy', từ đó suy ra xy//x'y'Vậy, chúng ta đã chứng minh được xy//x'y'
Câu hỏi liên quan:
- A. CÂU HỎI (TRẮC NGHIỆM)1. Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia On...
- 2.Trong các khẳng định sau, khẳng định nào đúng?A. Hai góc bằng nhau thì đối đỉnh;B. Hai góc...
- 3.Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc...
- 4. Hai đường thẳng cắt nhau tạo thành bốn góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào...
- 5.Hai đường thẳng AB và CD cắt nhau tại O. Cho Om là tia phân giác của góc BOD và$...
- 6.Cho Hình 3.29.a) Cặp góc so le trong là cặp góc:A. $\widehat{M1},\widehat{M2}$;B....
- 7.Cho Hình 3.30. Cặp góc A1, B1 là cặp góc:A. So le trong;B. Đối đỉnh;C. Đồng vị;D. Cả ba...
- 8.Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu:A....
- 9.Cho Hình 3.32, biết a//b. Khẳng định nào sau đâysai?A....
- 3.34.Cho Hình 3.34. Biết AB//Cx, $\widehat{A}=70^{\circ},\widehat{B}=60^{\circ}$. Tính số đo...
- 3.35.Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.a) Chứng minh rằng CN//AB.b) Tính số...
- 3.36.Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox//AB. Biết $\widehat{B}=40^{\circ}...
- 3.37.Trong Hình 3.37 có BE//AC, CF//AB. Biết $\widehat{A}=80^{\circ},\widehat{ABC}=6...






Dựa vào điều kiện đồng quy của các cặp đường thẳng, ta có thể dùng hình vẽ và phép biến đổi để chứng minh xy//x'y'.
Áp dụng định lí Euclid và dùng tính chất về tỉ số đồng quy, ta có thể chứng minh xy//x'y' theo cách khác.
Sử dụng tính chất của góc và cặp góc tương đồng, ta có thể chứng minh được xy//x'y' trong trường hợp tương ứng.
Chúng ta có thể sử dụng định lí Thales để chứng minh xy//x'y', với điều kiện là x,y,v' cùng thuộc một đường thẳng.
Để chứng minh xy//x'y', ta cần chứng minh tỉ số đồng quy của các cặp cạnh tương ứng trong hai tam giác xyv và x'y'v'.