3.37.Trong Hình 3.37 có BE//AC, CF//AB. Biết $\widehat{A}=80^{\circ},\widehat{ABC}=6...
Câu hỏi:
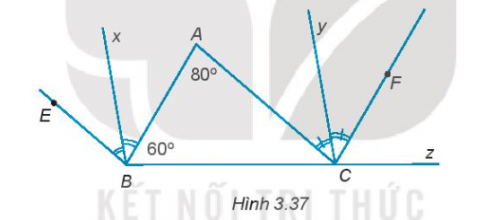
3.37. Trong Hình 3.37 có BE//AC, CF//AB. Biết $\widehat{A}=80^{\circ},\widehat{ABC}=60^{\circ}$.
a) Chứng minh rằng $\widehat{ABE}=\widehat{ACF}$.
b) Tính số đo của các góc BCF và ACB.
c) Gọi Bx, Cy lần lượt là tia phân giác của các góc ABE và ACF. Chứng minh rằng Bx//Cy.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Việt
Phương pháp giải:
a) Vì Bx là tia phân giác của góc ABE nên $\widehat{EBx}=\frac{1}{2}\widehat{EBA}=\frac{1}{2} \times 80^{\circ} = 40^{\circ}$.
Tương tự, vì Cy là tia phân giác của góc ACF nên $\widehat{ACy}=\frac{1}{2}\widehat{ACF}=\frac{1}{2} \times 80^{\circ} = 40^{\circ}$.
Ta có $\widehat{ABE} = \widehat{ACF}$.
b) Góc BCF kề bù với góc FCz nên $\widehat{BCF}=180^{\circ}-\widehat{FCz}=180^{\circ}-60^{\circ}=120^{\circ}$.
Với $\widehat{ACB} = \widehat{BCF} - \widehat{ACF} = 120^{\circ} - 80^{\circ} = 40^{\circ}$.
c) Ta có $\widehat{EBx}=\widehat{yCF}=40^{\circ}$, từ đó $\widehat{zBx} = \widehat{zCy} = 100^{\circ}$.
Vậy ta có Bx//Cy.
Vậy câu trả lời đầy đủ và chi tiết:
a) $\widehat{ABE} = \widehat{ACF}$.
b) $\widehat{BCF} = 120^{\circ}$, $\widehat{ACB} = 40^{\circ}$.
c) Bx//Cy.
a) Vì Bx là tia phân giác của góc ABE nên $\widehat{EBx}=\frac{1}{2}\widehat{EBA}=\frac{1}{2} \times 80^{\circ} = 40^{\circ}$.
Tương tự, vì Cy là tia phân giác của góc ACF nên $\widehat{ACy}=\frac{1}{2}\widehat{ACF}=\frac{1}{2} \times 80^{\circ} = 40^{\circ}$.
Ta có $\widehat{ABE} = \widehat{ACF}$.
b) Góc BCF kề bù với góc FCz nên $\widehat{BCF}=180^{\circ}-\widehat{FCz}=180^{\circ}-60^{\circ}=120^{\circ}$.
Với $\widehat{ACB} = \widehat{BCF} - \widehat{ACF} = 120^{\circ} - 80^{\circ} = 40^{\circ}$.
c) Ta có $\widehat{EBx}=\widehat{yCF}=40^{\circ}$, từ đó $\widehat{zBx} = \widehat{zCy} = 100^{\circ}$.
Vậy ta có Bx//Cy.
Vậy câu trả lời đầy đủ và chi tiết:
a) $\widehat{ABE} = \widehat{ACF}$.
b) $\widehat{BCF} = 120^{\circ}$, $\widehat{ACB} = 40^{\circ}$.
c) Bx//Cy.
Câu hỏi liên quan:
- A. CÂU HỎI (TRẮC NGHIỆM)1. Cho hai góc kề bù AOB và BOC. Tia OM nằm giữa hai tia OB và OC. Tia On...
- 2.Trong các khẳng định sau, khẳng định nào đúng?A. Hai góc bằng nhau thì đối đỉnh;B. Hai góc...
- 3.Hai đường thẳng cắt nhau tạo thành bốn góc khác góc bẹt. Biết số đo của một trong bốn góc...
- 4. Hai đường thẳng cắt nhau tạo thành bốn góc bẹt. Số đo của bốn góc đó có thể là trường hợp nào...
- 5.Hai đường thẳng AB và CD cắt nhau tại O. Cho Om là tia phân giác của góc BOD và$...
- 6.Cho Hình 3.29.a) Cặp góc so le trong là cặp góc:A. $\widehat{M1},\widehat{M2}$;B....
- 7.Cho Hình 3.30. Cặp góc A1, B1 là cặp góc:A. So le trong;B. Đối đỉnh;C. Đồng vị;D. Cả ba...
- 8.Cho Hình 3.31, đường thẳng a song song với đường thẳng b nếu:A....
- 9.Cho Hình 3.32, biết a//b. Khẳng định nào sau đâysai?A....
- B - BÀI TẬP3.33.Cho Hình 3.33. Hãy chứng minh xy//x'y'
- 3.34.Cho Hình 3.34. Biết AB//Cx, $\widehat{A}=70^{\circ},\widehat{B}=60^{\circ}$. Tính số đo...
- 3.35.Cho Hình 3.35. Biết CN là tia phân giác của góc ACM.a) Chứng minh rằng CN//AB.b) Tính số...
- 3.36.Cho Hình 3.36. Bên trong góc BOD vẽ tia Ox//AB. Biết $\widehat{B}=40^{\circ}...






{
"content1": "a) Ta có $\widehat{ABE} = \widehat{ABC} = 60^{\circ}$ (do BE//AC và AB là phân giác của $\widehat{A}$). Tương tự, $\widehat{ACF} = \widehat{A} = 80^{\circ}$. Vậy ta có $\widehat{ABE} = \widehat{ACF}$.",
"content2": "b) Góc BCF là $\widehat{BCF} = \widehat{A} = 80^{\circ}$ (do CF//AB). Góc ACB là $\widehat{ACB} = 180^{\circ} - \widehat{A} - \widehat{ABC} = 40^{\circ}$.",
"content3": "c) Ta có $\widehat{ABE} = \widehat{ABC} = 60^{\circ}$ và $\widehat{ACF} = \widehat{A} = 80^{\circ}$. Góc BEx và CyA là góc phân giác của góc $\widehat{A}$ nên Bx//Cy."
}