5.15Cho hệ vật như hình 5.1. Ban đầu hai vật được giữ sao cho lò xo bị nén một đoạn 10,0 cm...
Câu hỏi:
5.15 Cho hệ vật như hình 5.1. Ban đầu hai vật được giữ sao cho lò xo bị nén một đoạn 10,0 cm (lò xo nhẹ và không gắn vào vật) sau đó đốt sợi dây nối hai vật. Biết độ cứng của lò xo k = 45,0 N/m; m$_{1}$ = 0,50 kg; m$_{2}$ = 1,50 kg. Bỏ qua lực ma sát và lực cản của không khí tác dụng lên các vật.
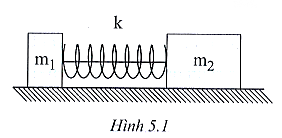
a) Tính gia tốc của mỗi vật ngay sau khi sợi dây đứt.
b) Biết rằng khi hai vật rời nhau thì m$_{1}$ chuyển động với tốc độ là 3,00 m/s. Tính tốc độ của m$_{2}$.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Vương
Phương pháp giải:a) Để tính gia tốc của mỗi vật sau khi sợi dây đứt, ta cần tính lực đàn hồi của lò xo tác dụng lên mỗi vật. Sau đó, áp dụng định luật Newton để tính gia tốc của mỗi vật.b) Để tính tốc độ của vật m$_{2}$ sau khi vật m$_{1}$ rời khỏi nó, ta sử dụng định luật bảo toàn động lượng.Câu trả lời đầy đủ và chi tiết hơn:a) Gia tốc của m$_{1}$ sau khi sợi dây đứt: $a_{1} = \frac{F_{1}}{m_{1}} = \frac{k\Delta x}{m_{1}} = \frac{45.0 \times 0.1}{0.5} = 9 \, \text{m/s}^2$Gia tốc của m$_{2}$ sau khi sợi dây đứt:$a_{2} = \frac{F_{2}}{m_{2}} = \frac{k\Delta x}{m_{2}} = \frac{45.0 \times 0.1}{1.5} = 3 \, \text{m/s}^2$b) Tốc độ của vật m$_{2}$ sau khi vật m$_{1}$ rời khỏi nó:Theo định luật bảo toàn động lượng:$m_{1}v_{1}+m_{2}v_{2} = 0$$v_{2} = \frac{-m_{1}v_{1}}{m_{2}} = \frac{-0.5 \times 3}{1.5} = -1 \, \text{m/s}$Vậy sau khi vật m$_{1}$ rời khỏi vật m$_{2}$, vật m$_{2}$ sẽ di chuyển với vận tốc là 1 m/s theo hướng ngược lại vật m$_{1}$ đang di chuyển.
Câu hỏi liên quan:
- 5.9 Trong phòng thí nghiệm, vật nào sau đây đang bị biến dạng kéo?A. Lò xo trong lực kế ống đang đo...
- 5.10Lực đàn hồi nói chung và lực đàn hồi của lò xo nói riêng có rất nhiều ứng dụng quan trọng...
- 5.11Một lò xo nhẹ có độ cứng k = 100 N/m và chiều dài tự nhiên l$_{o}$= 10,0 cm. Người...
- 5.12 Khi treo vào đầu dưới của một lò xo vật khối lượng m$_{1}$= 800 g thì lò xo có chiều dài...
- 5.13Một diễn viên xiếc đang leo lên một sợi dây được treo thẳng đứng từ trần nhà cao. Sợi dây...
- 5.14Một lò xo có độ cứng k = 400 N/m một đầu gắn cố định. Tác dụng một lực vào đầu còn lại...
- 5.16Cho các dụng cụ sau:Giá thí nghiệm đã gắn thước đo độ dài: 1 cái.Lò xo chưa biết độ cứng:...
- 5.17Cho các dụng cụ sau:Lực kế: 1 cái.Thước đo độ dài: 1 cáiLò xo cần xác định độ cứng: 1...
- 5.18 Một nhóm học sinh tìm hiểu độ cứng của lò xo. Họ dùng các lò xo giống nhau có cùng chiều dài...
Bình luận (0)





