2. Định lí Thales trong tam giácLuyện tập 3 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT:...
Câu hỏi:
2. Định lí Thales trong tam giác
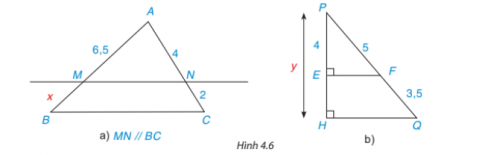
Luyện tập 3 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Tìm các độ dài x, y trong hình 4.6
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ánh
Phương pháp giải:a) Ta có hai đường thẳng MN và BC song song (do góc AMB và góc ANC cùng là góc phẩy trên hai đường thẳng MN và BC). Do đó, áp dụng định lí Thales, ta có tỷ lệ:$\frac{AM}{MB}=\frac{AN}{NC}$$\Rightarrow \frac{6,5}{x}=\frac{4}{2}$$\Rightarrow x=3,25$b) Ta có hai đường thẳng FE và QH đều vuông góc với đường thẳng PH. Do đó, FE và QH là hai đường thẳng song song. Áp dụng định lí Thales, ta có tỷ lệ:$\frac{PE}{PH}=\frac{PF}{PQ}$$\Rightarrow \frac{4}{y}=\frac{5}{5+3,5}$$\Rightarrow y=6,8$Vậy, độ dài của x là 3,25 và y là 6,8.
Câu hỏi liên quan:
- 1. Đoạn thẳng tỉ lệCho Hình 4.2, em hãy thực hiện các hoạt động sau:Hoạt động 1 trang 77 sách giáo...
- Hoạt động 2 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Dùng thước thẳng, đo độ dài hai...
- Hoạt động 3 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: So sánh tỉ số tìm được trong hai...
- Luyện tập 1 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Tìm tỉ số của các cặp đoạn thẳng...
- Luyện tập 2 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC và một điểm B'...
- Hoạt động 4 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho $\Delta ABC$ có AB = 6 cm, AC...
- Bài tậpBài tập 4.1 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Tìm độ dài x, y trong Hình...
- Bài tập 4.2 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT:Tìm các cặp đường thẳng song...
- Bài tập 4.3 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT:Cho tam giác ABC, từ điểm D...
- Bài tập 4.4 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT: Cho tam giác ABC có trọng tâm G....
- Bài tập 4.5 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 KNTT:Để đo khoảng cách giữa hai vị...






Cách tiếp cận khác cho bài này là áp dụng định lý Pythagore vào tam giác ABC để tìm các tỷ lệ giữa các cạnh. Sau đó, sử dụng công thức tỷ lệ đồng dạng giữa các cặp đoạn để giải phương trình và xác định giá trị của x và y trong hình 4.6.
Từ hình 4.6, ta thấy tam giác ABC là tam giác vuông tại A. Do đó, ta có thể xác định các tỷ lệ đối với các đoạn AB, AC và BC. Từ đó, sử dụng công thức tỷ lệ đồng dạng giữa các cặp đoạn, ta có thể tính được giá trị của x và y.
Theo định lí Thales, trong tam giác vuông, đường cao chia tam giác vuông thành 2 tam giác vuông nhỏ có tỷ lệ đồng dạng với tam giác ban đầu. Áp dụng định lí này vào hình 4.6, ta có thể tính được các độ dài x, y.