10.15.Một hình lăng trụ đứng được ghép bởi một hình lăng trụ đứng tam giác và một hình hộp...
Câu hỏi:
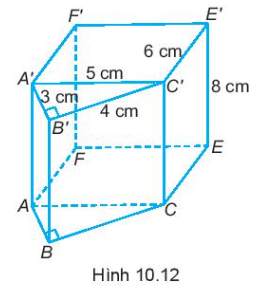
10.15. Một hình lăng trụ đứng được ghép bởi một hình lăng trụ đứng tam giác và một hình hộp chữ nhật có kích thước như trong Hình 10.12. Tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Ánh
Để tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’, ta cần tính thể tích của hình lăng trụ đứng ABC.A’B’C và thể tích của hình hộp chữ nhật ACEF.A’C’E’F’ trước.Phương pháp giải:- Thể tích hình lăng trụ đứng ABC.A’B’C là: $V1 = S \times h = (\frac{1}{2} \times 3 \times 4) \times 8 = 48 cm^{3}$- Thể tích hình hộp chữ nhật ACEF.A’C’E’F’ là: $V2 = 5 \times 6 \times 8 = 240 cm^{3}$- Thể tích hình lăng trụ đứng ABCEF.A’B’C’E’F’ là: $V = V1 + V2 = 48 + 240 = 288 cm^{3}$Vậy, thể tích của hình lăng trụ ABCEF.A’B’C’E’F’ là 288 $cm^{3}$.
Câu hỏi liên quan:
- BÀI TẬP10.9. Gọi tên đỉnh, cạnh đáy, cạnh bên, mặt đáy, mặt bên của hình lăng trụ đứng tứ giác...
- 10.10.Tính thể tích hình lăng trụ đứng tam giác trong Hình 10.8.
- 10.11.Một hình lăng trụ đứng đáy là một tứ giác có chu vi 30 cm, chiều cao của hình lăng trụ...
- 10.12.Một lăng kính thuỷ tinh có dạng hình lăng trụ đứng có đáy là tam giác đều, kích thước...
- 10.13.Một hình lăng trụ đứng có hình khai triển như Hình 10.10. Tính diện tích xung quanh của...
- 10.14.Cho hình lăng trụ đứng MNPQ.M’N’P’Q’ có đáy MNPQ là hình thang vuông tại M và N. Kích...






Để tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’, ta thực hiện các bước sau: Đầu tiên, tính diện tích đáy của hình lăng trụ tam giác bằng (1/2 * cơ sở * chiều cao). Tiếp theo, tính diện tích đáy của hình hộp chữ nhật bằng (chiều dài * chiều rộng). Sau đó, tính thể tích của hình lăng trụ tam giác và hình hộp chữ nhật rồi cộng lại để có thể tích của hình lăng trụ ABCEF.A’B’C’E’F’.
Để tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’, ta có thể phân tích vấn đề thành việc tính thể tích của hình lăng trụ tam giác và hình hộp chữ nhật rồi tổng hợp lại. Thể tích của hình lăng trụ tam giác được tính bằng (1/2 * b * h), trong đó b là cạnh của tam giác và h là chiều cao của tam giác. Thể tích của hình hộp chữ nhật được tính bằng (a * b * h), trong đó a và b là các cạnh của hình hộp và h là chiều cao của hình hộp.
Để tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’, ta có thể sử dụng các kích thước đã được cung cấp trong Hình 10.12 để tính toán. Trước tiên, tính thể tích của hình lăng trụ tam giác bằng (1/2 * cơ sở tam giác * chiều cao tam giác). Tiếp theo, tính thể tích của hình hộp chữ nhật bằng (diện tích đáy hình hộp * chiều cao hình hộp). Cuối cùng, cộng hai thể tích lại sẽ ra được kết quả cuối cùng.
Để tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’, ta cần tính thể tích của hình lăng trụ tam giác và hình hộp chữ nhật rồi cộng lại. Thể tích của hình lăng trụ tam giác được tính bằng công thức: (1/2 * diện tích đáy tam giác * chiều cao tam giác). Thể tích của hình hộp chữ nhật được tính bằng công thức: (diện tích đáy hình hộp * chiều cao hình hộp). Sau đó cộng hai thể tích lại sẽ ra được thể tích của hình lăng trụ ABCEF.A’B’C’E’F’.