Luyện tập 1 trang 32 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABC có SA =...
Câu hỏi:
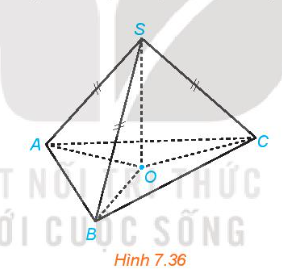
Luyện tập 1 trang 32 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
c) Chứng minh rằng nếu $AO \perp BC$ thì$ SA \perp BC.$
d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC)
Câu trả lời:
Người trả lời: GV. Đỗ Thị Linh
a) Ta có SA = SB = SC, vì vậy OA, OB, OC đều nằm trên đường trung trực của đoạn thẳng BC, CA, AB tương ứng. Khi đó, OA = OB = OC và O nằm trên đường trung trực của đoạn thẳng BC, CA, AB, cho nên O là tâm của đường tròn ngoại tiếp tam giác ABC.
b) Hình chiếu của đường thẳng SA trên mặt phẳng (ABC) là đoạn thẳng AB, vì SA vuông góc với mặt phẳng (ABC) và AB là một cạnh của tam giác đều ABC.
c) Nếu $AO \perp BC$, tức là AO vuông góc với BC, thì ta có SA vuông góc với BC.
d) Gọi M, N, P lần lượt là hình chiếu vuông góc của S lên BC, CA, AB. Do SA vuông góc với OM và SA song song với đường thẳng d nên d cũng vuông góc với OM. Khi đó, hình chiếu của tam giác SBC lên mặt phẳng (ABC) là tam giác có đỉnh M và đường cao là đường thẳng d. Tương tự, ta có thể tìm hình chiếu của tam giác SCA lên (ABC) là tam giác có đỉnh N và đường cao là đường thẳng e, cũng như tìm hình chiếu của tam giác SAB lên (ABC) là tam giác có đỉnh P và đường cao là đường thẳng f.
b) Hình chiếu của đường thẳng SA trên mặt phẳng (ABC) là đoạn thẳng AB, vì SA vuông góc với mặt phẳng (ABC) và AB là một cạnh của tam giác đều ABC.
c) Nếu $AO \perp BC$, tức là AO vuông góc với BC, thì ta có SA vuông góc với BC.
d) Gọi M, N, P lần lượt là hình chiếu vuông góc của S lên BC, CA, AB. Do SA vuông góc với OM và SA song song với đường thẳng d nên d cũng vuông góc với OM. Khi đó, hình chiếu của tam giác SBC lên mặt phẳng (ABC) là tam giác có đỉnh M và đường cao là đường thẳng d. Tương tự, ta có thể tìm hình chiếu của tam giác SCA lên (ABC) là tam giác có đỉnh N và đường cao là đường thẳng e, cũng như tìm hình chiếu của tam giác SAB lên (ABC) là tam giác có đỉnh P và đường cao là đường thẳng f.
Câu hỏi liên quan:
- 1. PHÉP CHIẾU VUÔNG GÓCHoạt động 1 trang 38 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Trên...
- Hoạt động 2 trang 39 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho đường thẳng a và mặt...
- 2. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNGHoạt động 3 trang 40 sách giáo khoa (SGK) toán lớp 11 tập 2...
- Vận dụng trang 41 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Tâm Trái Đất chuyển động quanh...
- Khám phá trang 42 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho đường thẳng $\Delta$ vuông...
- Trải nghiệm trang 42 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Đo góc giữa một sợi dây kéo...
- BÀI TẬPBài tập 7.10 trang 42 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABC...
- Bài tập 7.11 trang 42 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình chóp S.ABCD có đáy...
- Bài tập 7.12 trang 42 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình đóp S.ABC có SA....
- Bài tập 7.13 trang 43 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho điểm S nằm ngoài mặt...
- Bài tập 7.14 trang 43 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Trong một khoảng thời gian...
- Bài tập 7.15 trang 43 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Hãy nêu cách đo góc giữa...
Bình luận (0)





