Bài tập 6.23. Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến...
Câu hỏi:
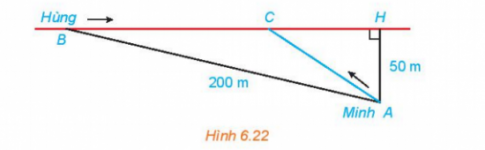
Bài tập 6.23. Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B, cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười).
Câu trả lời:
Người trả lời: GV. Đỗ Thị Huy
Để giải bài toán trên, ta thực hiện các bước sau:1. Đặt CH = x (x > 0)2. Tính AC = √(x^2 + 50^2) = √(x^2 + 2500)3. Tính BH = √(200^2 - 50^2) = 50√154. Tính BC = BH - CH = 50√15 - x5. Vì hai bạn gặp nhau tại C, nên thời gian đi từ A đến C bằng thời gian đi từ B đến C, suy ra:(50√15 - x) / 15 = √(x^2 + 2500) / 56. Giải phương trình trên ta được: 8x^2 + 100√15x - 15000 = 07. Giải phương trình trên ta được x ≈ 25.4 hoặc x ≈ -73.8, nhưng x > 0 nên x ≈ 25.48. Vị trí điểm C là cách H 1 khoảng 25.4 m.Vậy câu trả lời cho câu hỏi trên là: Vị trí điểm C là cách điểm H khoảng 25.4 m.
Câu hỏi liên quan:






Vị trí C trên lề đường sẽ là điểm mà Minh đã đi bộ được trong thời gian 0.02 giờ, tức là vị trí C = vận tốc đi bộ của Minh x thời gian = 5 km/h x 0.02 giờ.
Với khoảng cách giữa hai bạn là 200m và vận tốc tương đối 10km/h, thời gian là: thời gian = 200m / 10 km/h = 0.02 giờ.
Thời gian hai bạn gặp nhau được tính bằng công thức: thời gian = khoảng cách / vận tốc tương đối.
Vì vận tốc tương đối âý là âm, nghĩa là hai bạn đang tiếp cận nhau nên vận tốc này là vận tốc gần đến nhau.
Vận tốc tương đối giữa Hai bạn là vận tốc của Minh trừ đi vận tốc của Hùng: 5 km/h - 15 km/h = -10 km/h.