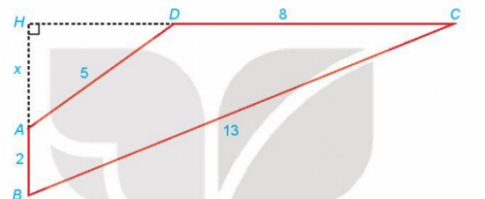
Bài tập 6.22. Cho tứ giác ABCD có AB $\bot $ CD; AB = 2; BC = 13; CD = 8; DA = 5. Gọi H là giao...
Câu hỏi:
Bài tập 6.22. Cho tứ giác ABCD có AB $\bot $ CD; AB = 2; BC = 13; CD = 8; DA = 5. Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Vương
Để giải bài toán, chúng ta cần thực hiện các bước sau: 1. Sử dụng định lí Pythagore trong tam giác vuông AHD để tính độ dài của HD.2. Áp dụng định lí Pythagore trong tam giác vuông BHC để thiết lập phương trình và giải phương trình để tìm giá trị của x.3. Kiểm tra giá trị x tìm được và chọn giá trị thích hợp.4. Tính diện tích của tam giác HAD và tam giác HBC.5. Tính diện tích của tứ giác ABCD bằng cách lấy diện tích tam giác BHC trừ đi diện tích tam giác HAD. Câu trả lời cho câu hỏi trên là: Giá trị của x là 3, diện tích của tứ giác ABCD là 30 đơn vị diện tích.
Câu hỏi liên quan:






Áp dụng định lý Pythagore trong tam giác AHĐ ta có: AC^2 + CD^2 = AD^2. Thay vào giá trị ta tìm được x = 1 và từ đó tính diện tích của tứ giác ABCD.
Từ đó suy ra AC.BD = 46. Giả sử AH = x thì BH = 2 - x và CD = 8 - x.
Thay các giá trị đã biết vào ta được: 2.8 + 13.5 = AC.BD
Ta có tứ giác ABCD là tứ giác nội tiếp nên sẽ áp dụng định lý Ptolemy: AB.CD + BC.DA = AC.BD