4.8. Tính tổng số đo $\widehat{A}+\widehat{C}$ trong Hình 4.8.
Câu hỏi:
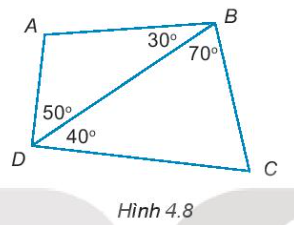
4.8. Tính tổng số đo $\widehat{A}+\widehat{C}$ trong Hình 4.8.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Đạt
Phương pháp giải:Để tính tổng số đo $\widehat{A}+\widehat{C}$ trong Hình 4.8, ta cần tìm số đo của góc $\widehat{A}$ và số đo của góc $\widehat{C$ trước đó.Với góc $\widehat{A}$, ta có: $\widehat{A}=180^{\circ}-50^{\circ}-30^{\circ}=100^{\circ}$Với góc $\widehat{C}$, ta có: $\widehat{C}=180^{\circ}-40^{\circ}-70^{\circ}=70^{\circ}$Do đó, tổng số đo $\widehat{A}+\widehat{C}=100^{\circ}+70^{\circ}=170^{\circ}$.Vậy câu trả lời cho câu hỏi "Tính tổng số đo $\widehat{A}+\widehat{C}$ trong Hình 4.8" là 170 độ.
Câu hỏi liên quan:
- BÀI TẬP4.1. Hãy tính các số đo các góc A, D, N trong tam giác dưới đây (H.4.3). Trong các tam...
- 4.2.Trong tam giác dưới đây (H.4.4), tam giác nào là nhọn, vuông, tù?
- 4.3.Tìm các số đo góc x, y trong Hình 4.5.
- 4.4.Tìm số đo các góc B và C của tam giác ABC trong Hình 4.6.
- 4.5.Tìm số đo góc x trong Hình 4.7.
- 4.6.Hãy viết các góc $\widehat{A},\widehat{B},\widehat{C}$ của tam giác ABC theo thứ tự tăng...
- 4.7.Hãy viết các góc $\widehat{A},\widehat{B},\widehat{C}$ của tam giác ABC theo thứ tự giảm...
- 4.9.Cho tam giác ABC thỏa mãn $\widehat{A}=\widehat{B}=2\widehat{C}$.a) Tính số đo các góc...






{ "Câu trả lời 1": "Theo công thức, tổng số đo của hai góc bất kỳ trong tam giác là 180 độ. Vì vậy, ta có: $\widehat{A} + \widehat{C} = 180^{\circ}$.", "Câu trả lời 2": "Góc $\widehat{A}$ và $\widehat{C}$ cùng nằm trên cùng một cạnh của tam giác, do đó tổng số đo của hai góc này là một góc phụ bên trong và bằng góc còn lại của tam giác, tức là $180^{\circ}$.", "Câu trả lời 3": "Ta biết rằng tổng số đo của bốn góc trong một tứ giác là $360^{\circ}$. Với tam giác như trong Hình 4.8, hai góc $\widehat{A}$ và $\widehat{C}$ tạo thành một góc phụ bên trong, do đó tổng số đo của hai góc này là $180^{\circ}$."}