Vận dụng 1.Cách đây 2000 năm, một nhà khoa học người Hy Lạp đã nghĩ ra cách đo chu vi Trái...

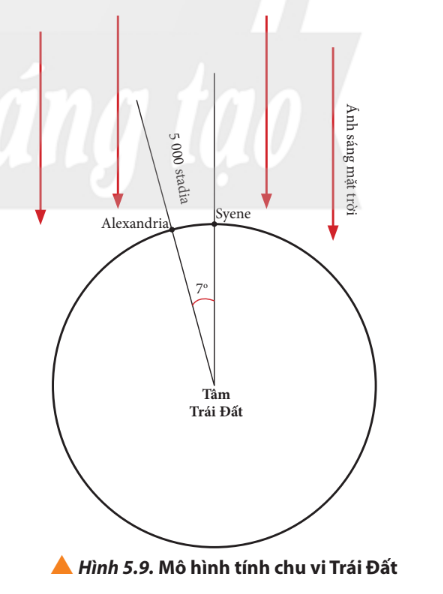
Vận dụng 1. Cách đây 2000 năm, một nhà khoa học người Hy Lạp đã nghĩ ra cách đo chu vi Trái Đất dựa vào bóng đổ của một cây gậy. Vào giữa trưa ngày hạ chí, ông nhận thấy rằng ánh sáng mặt trời chiếu xuống vuông góc thành phố Syene (thành phố Aswan ngày nay) nhưng không vuông góc ở Alexandria. Biết rằng hai thành phố này cách nhau khoảng 5000 stadia (1 stadia = 157 mét). Từ đó, ông đã tiến hành thí nghiệm bằng cách cắm một chiếc gậy thẳng đứng ở thành phố Alexandria vào ngày hạ chí. Vì ánh sáng mặt trời không chiếu vuông góc nên nó sẽ đổ bóng xuống mặt đất. Đo độ dài bóng của cây gậy và độ dài thực tế của gậy vào thời điểm Mặt Trời lên cao nhất, ông đã xác định được góc tạo bởi gậy và ánh sáng mặt trời là khoảng 7$^{o}$ (hình 5.9). Dựa vào số liệu trên, em hãy ước tính chu vi của Trái Đất là bao nhiêu. So sánh với số liệu thực tế ngày nay.