Luyện tập 1 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho tam giác MNP vuông tại N...
Câu hỏi:
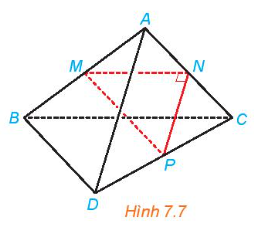
Luyện tập 1 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Cho tam giác MNP vuông tại N và một điểm A nằm ngoài mặt phẳng (MNP). Lần lượt lấy các điểm B, C, D sao cho M, N, P tương ứng là trung điểm của AB, AC, CD (H.7.7). Chứng minh rằng AD và BC vuông góc với nhau và chéo nhau.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Giang
Để chứng minh rằng AD và BC vuông góc với nhau và chéo nhau, ta có thể thực hiện theo các bước sau:1. Ta có tam giác MNP vuông tại N và M, N, P lần lượt là trung điểm của AB, AC, CD.2. Sử dụng định lí Pythagore trong tam giác vuông, ta có MN = 0.5AB, NP = 0.5AC, và MP = 0.5CD.3. Từ đó, ta có AB^2 + AC^2 = CD^2.4. Khi đó, ta thấy tam giác ABC và tam giác CDA là hai tam giác vuông cân có hình cắt đứt chúng theo đường trung trực.5. Gọi H là trung điểm của AB, ta có NH là đường trung trực của AB.6. Tương tự, DH là đường trung trực của CD.7. Khi đó, ta thấy rằng đường NH và DH cắt nhau tại một điểm O, là trung điểm của BC.8. Từ đó, ta chứng minh rằng AD và BC chéo nhau.9. Ngoài ra, NH vuông góc với AB, DH vuông góc với CD và BC vuông góc với NH.10. Do đó, ta chứng minh được rằng AD và BC vuông góc với nhau.Vậy, ta đã chứng minh được rằng AD và BC vuông góc với nhau và chéo nhau trong tam giác MNP và hình cắt tạo ra bởi AB, AC, CD.
Câu hỏi liên quan:
- 1. GÓC GIỮA HAI ĐƯỜNG THẲNGHoạt động 1 trang 28 sách giáo khoa (SGK) toán lớp 11 tập 2...
- Vận dụng trang 29 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Kim tự tháp Cheops là kim tự...
- 2. HAI ĐƯỜNG THẲNG VUÔNG GÓCHoạt động 2 trang 29 sách giáo khoa (SGK) toán lớp 11 tập 2...
- BÀI TẬPBài tập 7.1 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình lăng trụ...
- Bài tập 7.2 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho hình hộp ABCD.A'B'C'D'...
- Bài tập 7.3 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Cho tứ diện ABCD có...
- Bài tập 7.4 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT:Đối với nhà gỗ truyền thống,...
Bình luận (0)





