Giải bài tập toán lớp 11 tập 2 kết nối tri thức

CHƯƠNG VI. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT

CHƯƠNG VII. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN

CHƯƠNG VIII. CÁC QUY TẮC TÍNH XÁC SUẤT

CHƯƠNG IX. ĐẠO HÀM

1. GÓC GIỮA HAI ĐƯỜNG THẲNGHoạt động 1 trang 28 sách giáo khoa (SGK) toán lớp 11 tập 2...

Câu hỏi:

1. GÓC GIỮA HAI ĐƯỜNG THẲNG

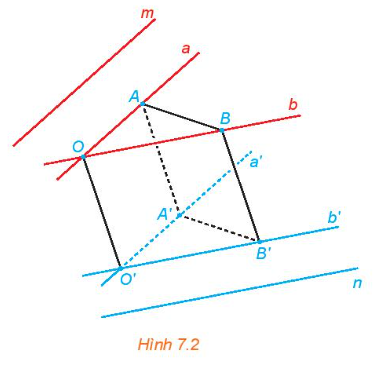
Hoạt động 1 trang 28 sách giáo khoa (SGK) toán lớp 11 tập 2 KNTT: Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a',b' tương ứng song song với m, n (H.7.2).

a) Mỗi cặp đường thẳng a, a và b, b' có cùng thuộc một mặt phẳng hay không?

b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A, đường thẳng qua B song song với OO' cắt b' tại B' Giải thích vì sao OAA'O', OBB'O', ABB'A' là các hình bình hành.

c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'. (Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B').

Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a',b' tương ứng song song với m, n (H.7.2).

Câu trả lời:
Người trả lời: GV. Đỗ Thị Ánh
Phương pháp giải:
a) Ta có hai đường thẳng song song a và a' đều cắt đường thẳng m tạo ra các góc đồng biên bằng nhau, và tương tự đối với b và b'. Do đó, cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng.

b) Vì OA // O'A' và OB // O'B', nên ta có OAA'O', OBB'O' là hai hình bình hành. Tương tự, với AB//A'B', ta có ABB'A' là một hình bình hành.

c) Áp dụng định lí côsin cho các tam giác OAB và O'A'B', ta có:
$cos(a,b) = \frac{OA}{OB}$ và $cos(a',b') = \frac{O'A'}{O'B'}$
Vì O'A' = OA và O'B' = OB do a', b' là các đường song song với a, b, nên ta có: $cos(a,b) = cos(a',b')$

Vậy, góc giữa hai đường thẳng a và b bằng góc giữa hai đường thẳng a' và b'.
Câu hỏi liên quan:
Bình luận (0)
Nhấn vào đây để đánh giá
Thông tin người gửi
Thông báoX
+ 5 điểm đăng nhập hằng ngày
0.06117 sec| 2179 kb