Bài tập 2.Lập phương trình mỗi đường thẳng trong các Hình 34, 35, 36, 37 sau đây:
Câu hỏi:
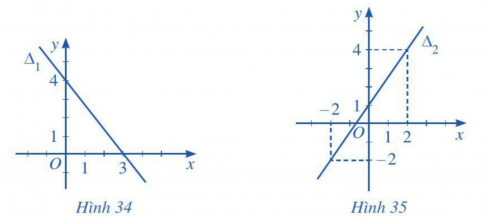
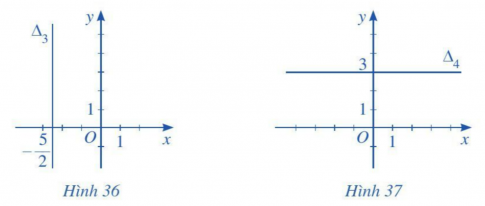
Bài tập 2. Lập phương trình mỗi đường thẳng trong các Hình 34, 35, 36, 37 sau đây:
Câu trả lời:
Người trả lời: GV. Đỗ Văn Việt
Để lập phương trình của mỗi đường thẳng trong các hình 34, 35, 36, 37, ta cần tìm vecto chỉ phương của đường thẳng đó và điểm đã biết trên đường thẳng để xác định phương trình.1. Đường thẳng trong Hình 34:- Điểm đã biết: A(3;0)- Vecto chỉ phương: $\overrightarrow{u} = (3; -4)$- Phương trình tham số: ${\Delta}_{1}: \begin{cases} x = 3 + 3t \\ y = -4t \end{cases}$2. Đường thẳng trong Hình 35:- Điểm đã biết: B(0;1)- Vecto chỉ phương: $\overrightarrow{u} = (4; 6)$- Phương trình tham số: ${\Delta}_{2}: \begin{cases} x = 4t \\ y = 1 + 6t \end{cases}$3. Đường thẳng trong Hình 36:- Điểm đã biết: C(-5/2; 0)- Vecto chỉ phương: $\overrightarrow{u} = (0; 1)$- Phương thức tham số: ${\Delta}_{3}: \begin{cases} x = -5/2 \\ y = t \end{cases}$4. Đường thẳng trong Hình 37:- Điểm đã biết: D(0;3)- Vecto chỉ phương: $\overrightarrow{u} = (1; 0)$- Phương thức tham số: ${\Delta}_{4}: \begin{cases} x = t \\ y = 3 \end{cases}$Vậy các phương trình của các đường thẳng trong các hình 34, 35, 36, 37 lần lượt là:1. ${\Delta}_{1}: \begin{cases} x = 3 + 3t \\ y = -4t \end{cases}$2. ${\Delta}_{2}: \begin{cases} x = 4t \\ y = 1 + 6t \end{cases}$3. ${\Delta}_{3}: \begin{cases} x = -5/2 \\ y = t \end{cases}$4. ${\Delta}_{4}: \begin{cases} x = t \\ y = 3 \end{cases}$
Câu hỏi liên quan:
- Bài tập 1.Lập phương trình tổng quát của đường thẳng $\Delta$ đi qua điểm A(-1;2) vàa....
- Bài tập 3.Cho đường thẳng d có phương trình tham số là:$\left\{ \begin{align}&...
- Bài tập 4.Cho đường thẳng d có phương trình tổng quát là: x - 2y - 5 = 0a. Lập phương trình...
- Bài tập 5.Cho tam giác ABC, biết A(1; 3); B(-1; -1); C(5; -3). Lập phương trình tổng quát...
- Bài tập 6.Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia...
Bình luận (0)





