10.Chứng minh rằng các đẳng thức sau đúng với mọi n∈ ℕ*
Câu hỏi:
10. Chứng minh rằng các đẳng thức sau đúng với mọi n∈ ℕ*
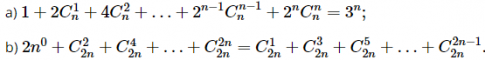
Câu trả lời:
Người trả lời: GV. Đỗ Văn Ngọc
Để chứng minh các đẳng thức trên, ta có thể sử dụng định lí nhị thức Newton hoặc áp dụng cách chứng minh bằng quy nạp.Phương pháp giải:a, Sử dụng định lí nhị thức Newton:$(a+b)^n = \sum_{k=0}^{n}C_{n}^{k}a^{n-k}b^k$Áp dụng vào đẳng thức cần chứng minh, ta có:$(1+2)^n = \sum_{k=0}^{n}C_{n}^{k}1^{n-k}2^k = 1C_{n}^{0}2^0 + 1C_{n}^{1}2^1 + ... + 1C_{n}^{n}2^n$Sau khi so sánh với biểu thức cần chứng minh, ta chứng minh được đẳng thức đúng với mọi n∈ ℕ*.b, Thay x = -1 vào $(x+1)^{2n}$ ta được $(-1+1)^{2n} = 0$Vậy ta chứng minh được đẳng thức trên với mọi nâng cao hơn.
Câu hỏi liên quan:
- 1. Chứng minh rằng các đẳng thức sau đúng với mọin$\epsilon N*$a,...
- 2. Chứng minh rằng với mọi n$\epsilon N*$a, $3^n$-1-2n chia hết chp 4b, $7^n$-$4^n$-$3^n$ chia hết...
- 3. Chứng minh rằng $8^n$ $\geq $ $n^3$ với mọi n $\epsilon N*$
- 4. Chứng minh rằng bất đẳng thức 1+ $\frac{1}{2}$ + $\frac{1}{3}$+...+ $\frac{1}{n}$ $\leq $...
- 5. Với một bình rỗng có dung tích 2l, một bạn học sinh thực hiện thí nghiệm theo các bước như...
- 6.Tìm hệ số của x3trong khai triển:a, $(1-3x)^8$b, $(1+\frac{x}{2})^7$
- 7.Tìm hệ số của $x^5$trong khai triển $(2x+3)(x-2)^2$
- 7.Tìm hệ số của $x^5$trong khai triển $(2x+3)(x-2)^2$
- 8.a)Tìm ba số hạng đầu tiên trong khai triển của $(1 + 2x)^6$, các số hạng được viết theo thứ...
- 9.Trong khai triển biểu thức $(3x – 4)^{15}$thành đa thức, hãy tính tổng các hệ số của...
Bình luận (0)





